 por jeff_95 » Dom Dez 01, 2013 17:04
por jeff_95 » Dom Dez 01, 2013 17:04
Exercicio do Stewart
![\int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}} \int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}}](/latexrender/pictures/7b72320f36d23c44722860db93423952.png)
Resposta : 1/6
Não consigo encontrar uma substituição adequada, se alguem puder me dar uma luz ...
-
jeff_95
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Nov 16, 2013 19:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecânica
- Andamento: cursando
 por e8group » Dom Dez 01, 2013 17:16
por e8group » Dom Dez 01, 2013 17:16
Bom vamos ter que impor que
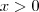
para a seguinte manipulação algébrica,mas não há problema quanto a isto , a remoção de um ponto não alterará o resultado da integral , segue
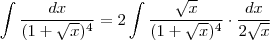
.
A substituição
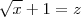
resolve o problema .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- integrais por substituiçao
por rita becher » Seg Mai 16, 2011 14:33
- 1 Respostas
- 1502 Exibições
- Última mensagem por DanielFerreira

Dom Mar 04, 2012 10:35
Funções
-
- [Integrais] Substituição
por dehcalegari » Qua Ago 07, 2013 09:34
- 2 Respostas
- 1028 Exibições
- Última mensagem por dehcalegari

Qua Ago 07, 2013 12:52
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Método da substituição
por Gabriel_1403 » Sáb Set 29, 2012 14:50
- 1 Respostas
- 1577 Exibições
- Última mensagem por MarceloFantini

Sáb Set 29, 2012 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Integrais por substituição trigonométrica
por Victor Mello » Seg Nov 11, 2013 23:13
- 3 Respostas
- 1869 Exibições
- Última mensagem por Victor Mello

Ter Nov 12, 2013 23:32
Cálculo: Limites, Derivadas e Integrais
-
- [Usando tecnicas de integrais por substituiçao simples]
por menino de ouro » Qua Out 24, 2012 23:10
- 1 Respostas
- 1688 Exibições
- Última mensagem por MarceloFantini

Qui Out 25, 2012 01:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}} \int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}}](/latexrender/pictures/7b72320f36d23c44722860db93423952.png)

![\int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}} \int_{0}^{1}\frac{dx}{{(1 + \sqrt[]{x})}^{4}}](/latexrender/pictures/7b72320f36d23c44722860db93423952.png)

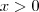 para a seguinte manipulação algébrica,mas não há problema quanto a isto , a remoção de um ponto não alterará o resultado da integral , segue
para a seguinte manipulação algébrica,mas não há problema quanto a isto , a remoção de um ponto não alterará o resultado da integral , segue 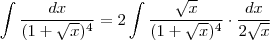 .
. 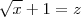 resolve o problema .
resolve o problema .
