 por vinicius_dlv » Qua Nov 25, 2009 13:10
por vinicius_dlv » Qua Nov 25, 2009 13:10
Olá colegas,
Eu estou estudando a parte de maximo e minimos locais com aplicações de Calculo 1. Eu tinha resolvido todos os problemas até agora com O Teste da Segunda Derivada. Entretanto, não estou conseguindo resolver esse problema da mesma maneira não sei porque. Ja tentei de tudo :
Ache todos os pontos da curva
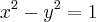
, mais próximo do ponto P(0,2). Resposta: ( -
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
, 1) , (
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
, 1)
-
vinicius_dlv
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Nov 25, 2009 12:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Máximo e mínimo
por thadeu » Qua Nov 18, 2009 13:47
- 1 Respostas
- 4169 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 17:50
Trigonometria
-
- [Maximo e Minimo]
por Scheu » Sex Mar 16, 2012 01:23
- 1 Respostas
- 2470 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:14
Cálculo: Limites, Derivadas e Integrais
-
- [Máximo & Minimo]
por allakyhero » Sáb Jun 30, 2012 12:41
- 6 Respostas
- 4925 Exibições
- Última mensagem por allakyhero

Dom Jul 01, 2012 11:06
Cálculo: Limites, Derivadas e Integrais
-
- máximo e minimo
por brunoguim05 » Qua Mai 28, 2014 15:26
- 0 Respostas
- 1551 Exibições
- Última mensagem por brunoguim05

Qua Mai 28, 2014 15:26
Geometria Analítica
-
- Otimização - Máximo e Mínimo
por elbert005 » Dom Jun 05, 2011 20:32
- 0 Respostas
- 4721 Exibições
- Última mensagem por elbert005

Dom Jun 05, 2011 20:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
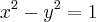 , mais próximo do ponto P(0,2). Resposta: ( -
, mais próximo do ponto P(0,2). Resposta: ( - ![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) , 1) , (
, 1) , ( ![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) , 1)
, 1)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.