Salve galera,
To com uma dúvida que não to conseguindo resolver, sei lá o que falta...
Olha esse exercicio:
A sucessão (1,a,b,27,c) é uma PG. Calcule a, b e c.
simplismente, não sei!
abraço a todos!



 é uma sequência geométrica de razão
é uma sequência geométrica de razão  se
se  e assim por diante . Por exemplo , as raízes
e assim por diante . Por exemplo , as raízes  do polinômio
do polinômio  é uma sequência geométrica de razão 2 . Pois podemos escrever ,
é uma sequência geométrica de razão 2 . Pois podemos escrever , 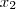 como
como  e
e 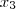 como
como  .
.
santhiago escreveu:Lembre-seé uma sequência geométrica de razão
se
e assim por diante . Por exemplo , as raízes
do polinômio
é uma sequência geométrica de razão 2 . Pois podemos escrever ,
como
e
como
.
Agora tente concluir e comente as dúvidas .

 . A sucessão
. A sucessão  é uma P.G . então existe um número real
é uma P.G . então existe um número real  constante tal que
constante tal que  . Só que
. Só que  ,assim encontrando
,assim encontrando  determinaremos
determinaremos 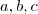 . E como sabemos que
. E como sabemos que  ,temos que pelo resultado acima
,temos que pelo resultado acima e portanto
e portanto  . Agora tente concluir.
. Agora tente concluir.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)