 por Pessoa Estranha » Dom Out 06, 2013 14:25
por Pessoa Estranha » Dom Out 06, 2013 14:25
Determine os complexos z tais que:
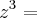
conjugado de

.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Taka » Dom Nov 03, 2013 09:23
por Taka » Dom Nov 03, 2013 09:23
Sendo z = a+bi, se

, e

, então temos:





Logo,

ou
![b=+\sqrt[]{\frac{{a}^{2}+3a-1}{3}} b=+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}](/latexrender/pictures/d268f4927ae0ee4c1c816ec610a713e5.png)
ou
![b=-\sqrt[]{\frac{{a}^{2}+3a-1}{3}} b=-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}](/latexrender/pictures/0e59812b48dd07e937bb01fc5ee58363.png)
.
Portanto,

ou
![z=a+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i z=a+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i](/latexrender/pictures/bb2498612424114710a908c3da7bb93d.png)
ou
![z=a-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i z=a-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i](/latexrender/pictures/3a5c7af11198d14469cce27ed8295cc0.png)
-
Taka
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Nov 02, 2013 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Química
- Andamento: cursando
 por Pessoa Estranha » Dom Nov 03, 2013 11:09
por Pessoa Estranha » Dom Nov 03, 2013 11:09
Valeu!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Aritmética] Números Complexos
por Pessoa Estranha » Dom Out 06, 2013 17:15
- 1 Respostas
- 2087 Exibições
- Última mensagem por PedroCunha

Qua Nov 27, 2013 22:01
Aritmética
-
- [Aritmética] Números Complexos
por Pessoa Estranha » Dom Out 06, 2013 17:17
- 0 Respostas
- 1218 Exibições
- Última mensagem por Pessoa Estranha

Dom Out 06, 2013 17:17
Aritmética
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17117 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13356 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10333 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
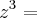 conjugado de
conjugado de  .
.
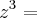 conjugado de
conjugado de  .
.
 , e
, e  , então temos:
, então temos:




 ou
ou ![b=+\sqrt[]{\frac{{a}^{2}+3a-1}{3}} b=+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}](/latexrender/pictures/d268f4927ae0ee4c1c816ec610a713e5.png) ou
ou ![b=-\sqrt[]{\frac{{a}^{2}+3a-1}{3}} b=-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}](/latexrender/pictures/0e59812b48dd07e937bb01fc5ee58363.png) .
. ou
ou ![z=a+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i z=a+\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i](/latexrender/pictures/bb2498612424114710a908c3da7bb93d.png) ou
ou ![z=a-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i z=a-\sqrt[]{\frac{{a}^{2}+3a-1}{3}}i](/latexrender/pictures/3a5c7af11198d14469cce27ed8295cc0.png)



 .
.



