 por fabriel » Sáb Nov 02, 2013 12:47
por fabriel » Sáb Nov 02, 2013 12:47
E ai pessoal estou há algum tempo tentando resolver essa integral, mas não obtive bom êxito.
é a seguinte integral:
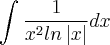
Se alguém conseguir resolve-lá por favor comente aqui
obrigado!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fabriel » Sáb Nov 02, 2013 17:58
por fabriel » Sáb Nov 02, 2013 17:58
Que complicado heim
Tenho certeza sim.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Sáb Nov 02, 2013 19:31
por e8group » Sáb Nov 02, 2013 19:31
Não conseguir obter resultados . Mas se aceitarmos que

e tomarmos

, obteremos

. Daí só integrar . E sgn é a função sinal . Se a integral fosse definida poderíamos obter resultados satisfatório (Acredito ).
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma questao complicada pra mim ;/
por hian » Dom Nov 14, 2010 16:50
- 1 Respostas
- 1628 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:33
Binômio de Newton
-
- Questão Complicada
por Kelvin Brayan » Dom Abr 24, 2011 11:01
- 2 Respostas
- 2889 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 15:01
Sistemas de Equações
-
- [questão complicada]
por JKS » Qui Jun 20, 2013 01:48
- 1 Respostas
- 2459 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 16:24
Números Complexos
-
- Equação Complicada #!!!
por Claudio Matos » Ter Ago 18, 2015 15:43
- 1 Respostas
- 1650 Exibições
- Última mensagem por nakagumahissao

Ter Ago 18, 2015 20:14
Equações
-
- Equacão um pouco complicada.
por gustavoluiss » Qua Nov 24, 2010 08:31
- 2 Respostas
- 1844 Exibições
- Última mensagem por davi_11

Qua Nov 24, 2010 12:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
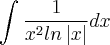

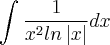



 e tomarmos
e tomarmos  , obteremos
, obteremos  . Daí só integrar . E sgn é a função sinal . Se a integral fosse definida poderíamos obter resultados satisfatório (Acredito ).
. Daí só integrar . E sgn é a função sinal . Se a integral fosse definida poderíamos obter resultados satisfatório (Acredito ).
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.