 por HCF01 » Sáb Out 26, 2013 13:38
por HCF01 » Sáb Out 26, 2013 13:38
Se |a|=3, |b|=4 e "a" forma com "b" um ângulo de 150º então |(a+3b)x(3a-b)| vale ?
Resposta: 60
Tentei utilizar o produto escalar e realizar as operações dentro do módulo, mas não sei como fazer isso devido ao produto vetorial. Gostaria de saber como ficariam as operações dentro do módulo.
-
HCF01
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Out 26, 2013 13:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Out 27, 2013 19:20
por Russman » Dom Out 27, 2013 19:20
Basta expandir o produto
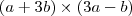
.
Faça,
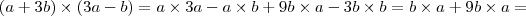
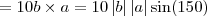
.
Só calcular.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por HCF01 » Seg Out 28, 2013 14:19
por HCF01 » Seg Out 28, 2013 14:19
Entendi. Muito obrigado, me ajudou bastante.
-
HCF01
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Out 26, 2013 13:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7371 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2990 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5213 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3406 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2380 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


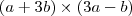 .
.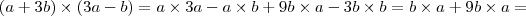
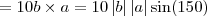 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.