 por darkthorn » Dom Out 20, 2013 09:25
por darkthorn » Dom Out 20, 2013 09:25
Boa tarde,
Ando aqui às voltas com este exercício e não consigo resolver o mesmo, será que me podem dar uma maozinha?
Considere o círculo trigonométrico representado no referencial o.n. Oxy da figura (da imagem), ao qual pertencem os pontos P e Q. Seja alfa a amplitude do ângulo POR e R o ponto de intersecção da semirecta OQ com a recta r, paralela ao eixo Oy e que intersecta o eixo Ox em P. Considere ainda o arco RS, centrado em P. A abcissa do ponto S em função de alfa é:
a) cos alfa - tg alfa b) 1+ tg alfa c) sen alfa - tg alfa d) 1-tg alfa

Uploaded with
ImageShack.usObrigada
-
darkthorn
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 20, 2013 09:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: formado
 por young_jedi » Dom Out 20, 2013 22:53
por young_jedi » Dom Out 20, 2013 22:53
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por darkthorn » Ter Out 29, 2013 23:44
por darkthorn » Ter Out 29, 2013 23:44
Muito obrigada Jedi

-
darkthorn
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 20, 2013 09:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular det(A-x.I)
por Bruhh » Sáb Jun 05, 2010 18:59
- 3 Respostas
- 4487 Exibições
- Última mensagem por MarceloFantini

Seg Jun 07, 2010 12:26
Matrizes e Determinantes
-
- (ITA) Calcular x + y
por Carolziiinhaaah » Qui Jun 24, 2010 14:47
- 3 Respostas
- 2644 Exibições
- Última mensagem por DanielFerreira

Ter Jun 29, 2010 16:37
Matrizes e Determinantes
-
- calcular:
por willwgo » Qui Mai 05, 2011 16:33
- 1 Respostas
- 1637 Exibições
- Última mensagem por FilipeCaceres

Qui Mai 05, 2011 19:51
Polinômios
-
- Calcular a.b
por -civil- » Ter Set 20, 2011 23:29
- 3 Respostas
- 2626 Exibições
- Última mensagem por MarceloFantini

Qui Set 29, 2011 21:07
Polinômios
-
- (Calcular)
por Veronica Souza » Ter Abr 24, 2012 13:06
- 6 Respostas
- 4319 Exibições
- Última mensagem por Fabiano Vieira

Seg Mai 28, 2012 23:30
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



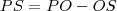
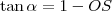
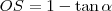




 , avisa que eu resolvo.
, avisa que eu resolvo.

