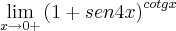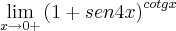por Danilo » Sáb Out 12, 2013 19:57
por Danilo » Sáb Out 12, 2013 19:57
Resolver
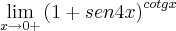
Substituindo 0 no limite eu não chego ao resultado, pois cotg 0 não existe... não tenho a menor idéia de como resolver este... Alguma idéia? Grato desde já...
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Sáb Out 12, 2013 23:32
por young_jedi » Sáb Out 12, 2013 23:32
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Danilo » Sáb Out 12, 2013 23:48
por Danilo » Sáb Out 12, 2013 23:48
Valeu cara, muito obrigado!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3119 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Duvida
por Claudin » Qua Mai 18, 2011 18:32
- 3 Respostas
- 2603 Exibições
- Última mensagem por Claudin

Qua Mai 18, 2011 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qua Mai 18, 2011 21:19
- 6 Respostas
- 3317 Exibições
- Última mensagem por Claudin

Qui Mai 19, 2011 12:31
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qui Mai 19, 2011 09:20
- 5 Respostas
- 3081 Exibições
- Última mensagem por Claudin

Dom Mai 22, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Sáb Mai 21, 2011 16:17
- 18 Respostas
- 10932 Exibições
- Última mensagem por Claudin

Qui Mai 26, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.