 por renan_cpime14 » Dom Set 29, 2013 10:34
por renan_cpime14 » Dom Set 29, 2013 10:34
Bom dia, no problema 1 do Exercício 7.7 do GUIDORIZZI - CALC 2 ( 5ªEd , p.143) temos que calcular o comprimento da curva dada:
na letra c temos que:
![\gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi] \gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi]](/latexrender/pictures/99acdebcd051384e61cccd716c6d65d3.png)
desenvolvi e travei nessa integral abaixo:
![\int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt \int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt](/latexrender/pictures/38fb2bab62d0b438aafb68c1d58ed022.png)
gostaria que alguém me ajudasse a resolver.
1) tenho que transformar em uma substituição trigonométrica, portanto
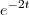
substituirei por
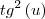
, logo, teremos
![\sqrt[]{{tg^{2} \left(u \right)}+ 1} \sqrt[]{{tg^{2} \left(u \right)}+ 1}](/latexrender/pictures/088411e6a74e19a508562777e40598f7.png)
que resultará em
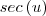
Para isso
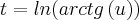
e
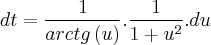
Os limites serão
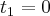
será
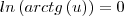
que será
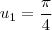
e
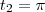
será
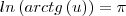
, logo
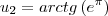
Gostaria de saber se há algum passo errado e como faço pra achar essa integral:
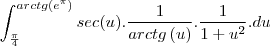
-
renan_cpime14
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Set 29, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Concurso engenharia
- Andamento: cursando
 por young_jedi » Dom Set 29, 2013 14:04
por young_jedi » Dom Set 29, 2013 14:04
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3684 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Cálculo de integral
por LAZAROTTI » Dom Set 30, 2012 19:52
- 0 Respostas
- 1196 Exibições
- Última mensagem por LAZAROTTI

Dom Set 30, 2012 19:52
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3276 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3173 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi] \gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi]](/latexrender/pictures/99acdebcd051384e61cccd716c6d65d3.png)
![\int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt \int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt](/latexrender/pictures/38fb2bab62d0b438aafb68c1d58ed022.png)
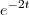 substituirei por
substituirei por 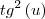 , logo, teremos
, logo, teremos ![\sqrt[]{{tg^{2} \left(u \right)}+ 1} \sqrt[]{{tg^{2} \left(u \right)}+ 1}](/latexrender/pictures/088411e6a74e19a508562777e40598f7.png) que resultará em
que resultará em 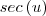
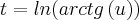 e
e 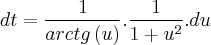
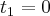 será
será 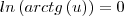 que será
que será 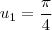 e
e 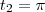 será
será 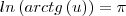 , logo
, logo 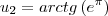
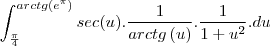


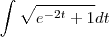
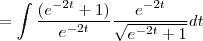
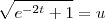
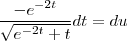
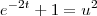
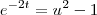
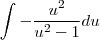
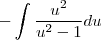
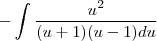
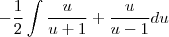
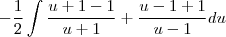
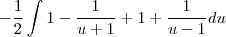
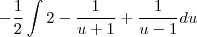
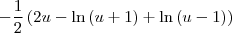
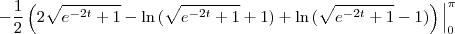

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.