 por joao_neto » Qua Set 25, 2013 00:07
por joao_neto » Qua Set 25, 2013 00:07
(Unifor-CE) A equação da circunferência que contém a origem, tem centro na reta x=2 e tangencia a reta x + y -4 = 0 é:
a) x² + y² + 4x - 4y + 4 = 0
b) x² + y² - 2x + 2y = 0
c) x² + y² - 4x + 4y = 0
d) x² + y² + 4x - 4y = 0
e) x² + y² - 4x + 4y + 4 = 0
A minha dificuldade nessa questão está em achar o y do centro, afinal para qualquer valor de y x valeria 2, assim y poderia assumir qualquer valor?
-
joao_neto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 21, 2013 17:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Set 25, 2013 15:47
por Russman » Qua Set 25, 2013 15:47
Primeiramente, para conter a origem a equação da circunferência deve se anular para (x,y)=(0,0). Certo? Então as alternativas a) e e) não podem ser as corretas. Agora, se o centro da circunferência está na reta x=2 então a coordenada x do centro é 2 e a equação pode ser escrita como
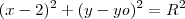
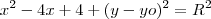
.
Agora, já que os únicos termos qe tem x já estão expostos você deve deduzir q a opção correta é a letra c) pois somente ela tem "-4" multiplicando o x.
Porém, se você prefere resolver completamente a questão, podemos usar a infirmação de que
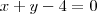
é tangente a circunferência. Note que o raio
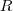
é a distância entre o centro e a própria reta. Portanto,
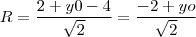
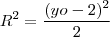
e, assim
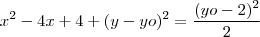
ou
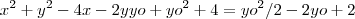
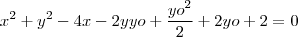
Agora, novamente, como
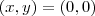
deve estar na circunferência então
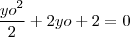
de onde
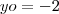
.
Logo,
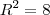
e
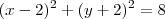
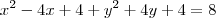
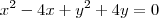
que é a alternativa c) .
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por joao_neto » Qua Set 25, 2013 23:57
por joao_neto » Qua Set 25, 2013 23:57
Sua explicação foi ótima, entendi perfeitamente. Muito obrigado!

-
joao_neto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 21, 2013 17:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11059 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida sobre PA
por Cleyson007 » Ter Mai 27, 2008 23:22
- 3 Respostas
- 5012 Exibições
- Última mensagem por admin

Sáb Mai 31, 2008 21:57
Progressões
-
- duvida sobre mmc e mdc
por edson cesar » Ter Dez 07, 2010 09:10
- 0 Respostas
- 2085 Exibições
- Última mensagem por edson cesar

Ter Dez 07, 2010 09:10
Sistemas de Equações
-
- Duvida sobre EDO
por manolo223 » Dom Nov 13, 2011 00:19
- 2 Respostas
- 2431 Exibições
- Última mensagem por manolo223

Dom Nov 13, 2011 13:07
Cálculo: Limites, Derivadas e Integrais
-
- duvida sobre x' e x''
por Debylow » Ter Dez 04, 2012 16:57
- 1 Respostas
- 1588 Exibições
- Última mensagem por Russman

Ter Dez 04, 2012 19:06
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


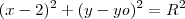
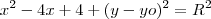 .
.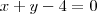 é tangente a circunferência. Note que o raio
é tangente a circunferência. Note que o raio 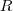 é a distância entre o centro e a própria reta. Portanto,
é a distância entre o centro e a própria reta. Portanto,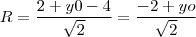
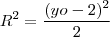
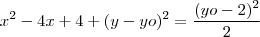
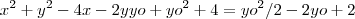
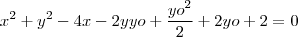
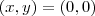 deve estar na circunferência então
deve estar na circunferência então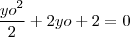
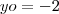 .
.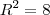 e
e 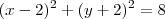
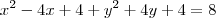
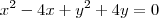


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: