 por raimundoocjr » Ter Set 24, 2013 20:40
por raimundoocjr » Ter Set 24, 2013 20:40
(Livro: Cálculo - Volume 2 - 7ª Edição - Q. 31 - Pág.: 767) Determine as equações paramétricas da reta r tangente à curva d(t)=(t cost, t, t sent), t>0 ou t=0, no ponto P=(-pi, pi, 0). Esboce em um mesmo sistema de coordenadas retangular tridimensional a trajetória da curva d, o ponto P e a reta r.
Como faço isso?
-
raimundoocjr
-
 por Russman » Ter Set 24, 2013 22:13
por Russman » Ter Set 24, 2013 22:13
Lembre-se que o vetor diretor de uma reta tangente a uma curva é sempre perpendicular ao vetor normal da mesma. Ainda que para obter, por exemplo,
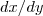
basta dividir
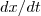
por
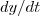
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por raimundoocjr » Qua Set 25, 2013 19:05
por raimundoocjr » Qua Set 25, 2013 19:05
Não fiz um ensaio ou tratado da minha dúvida porque trata da própria essência da questão. Então, poderia deixar mais claro a resolução desse exercício em específico? As próximas atividades que forem semelhantes a essa, eu já faço com mais segurança. Obrigado por responder.
-
raimundoocjr
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3436 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equaçoes parametricas
por angels900 » Ter Jan 31, 2012 14:35
- 6 Respostas
- 3741 Exibições
- Última mensagem por LuizAquino

Ter Jan 31, 2012 17:04
Geometria Analítica
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2123 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- Faz sentido? Sistema e equações paramétricas.
por Dan » Ter Fev 01, 2011 14:39
- 4 Respostas
- 3764 Exibições
- Última mensagem por LuizAquino

Qua Fev 02, 2011 11:37
Sistemas de Equações
-
- Geometria Analítica Equações Paramétricas.
por lucat28 » Sex Set 16, 2011 19:08
- 1 Respostas
- 1414 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 19:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

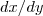 basta dividir
basta dividir 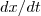 por
por 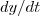 .
.