(USP) Simplifique:
![\sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}}](/latexrender/pictures/1cec2a67a0cfed29fa364d9b4a198997.png)
Fazendo eu cheguei a isso:
![\sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}} \sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}}](/latexrender/pictures/23b21317c50f3e70e5ab9df2a471c2a4.png) =>
=>=
![\sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})}](/latexrender/pictures/d633042033fe640219efd61c667d9c49.png) =>
=>=
![\sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})}](/latexrender/pictures/da88b4ba4d376d828a6756b1bcef00b6.png) =>
=>=
![\sqrt[2]{63+27\sqrt[2]{3}} \sqrt[2]{63+27\sqrt[2]{3}}](/latexrender/pictures/b7a017c5ada2ba3e612a65df155868a7.png) =>
=>Enquanto o gabarito que me foi dado diz que o resultado seria:
![3\sqrt[2]{5+\sqrt[2]{3}} 3\sqrt[2]{5+\sqrt[2]{3}}](/latexrender/pictures/5f5e7b6389df69bbadb03ae53a86535d.png) =>
=> ![\sqrt[2]{45+9\sqrt[2]{3}} \sqrt[2]{45+9\sqrt[2]{3}}](/latexrender/pictures/3604ee945cbe7386099ab0698c90c716.png)
Vocês podem me dizer onde raios foi que eu errei? Obrigado.

![\sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}}](/latexrender/pictures/1cec2a67a0cfed29fa364d9b4a198997.png)
![\sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}} \sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}}](/latexrender/pictures/23b21317c50f3e70e5ab9df2a471c2a4.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})}](/latexrender/pictures/d633042033fe640219efd61c667d9c49.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})}](/latexrender/pictures/da88b4ba4d376d828a6756b1bcef00b6.png) =>
=>![\sqrt[2]{63+27\sqrt[2]{3}} \sqrt[2]{63+27\sqrt[2]{3}}](/latexrender/pictures/b7a017c5ada2ba3e612a65df155868a7.png) =>
=>![3\sqrt[2]{5+\sqrt[2]{3}} 3\sqrt[2]{5+\sqrt[2]{3}}](/latexrender/pictures/5f5e7b6389df69bbadb03ae53a86535d.png) =>
=> ![\sqrt[2]{45+9\sqrt[2]{3}} \sqrt[2]{45+9\sqrt[2]{3}}](/latexrender/pictures/3604ee945cbe7386099ab0698c90c716.png)

![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)](/latexrender/pictures/e89eab6fc99912f4a593ad52552b441e.png)

Pessoa Estranha escreveu:Olá. Você cometeu um pequeno erro de sinal. Observe o seguinte:
![(9-3+\sqrt[2]{3}) (9-3+\sqrt[2]{3})](/latexrender/pictures/399524712f54ca5abeea655608f31cf2.png)

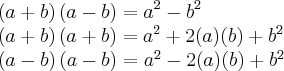

![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}}) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}})](/latexrender/pictures/8fc59f59a91c6ff5e46bdb52a93bb39d.png)

Pessoa Estranha escreveu:Você pode até fazer o processo da distributiva. Assim:
![6+\sqrt[2]{3} 6+\sqrt[2]{3}](/latexrender/pictures/f80cf9b7665bd683150468a02d903a05.png)
![9-3-\sqrt[2]{3} 9-3-\sqrt[2]{3}](/latexrender/pictures/3eb686d0694193733895a86810393ebb.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)