Olá Ananda, bom dia!
Ótimo!
Apenas para expandir o conteúdo, vou comentar uma alternativa para esta sua prática e correta conclusão:
Como a área lateral do cone obtido e a do tronco são iguais, a área lateral do cone obtido deve ser a metade da área do cone original.
Com isso:
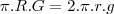
Primeiro, vamos mostrar como obter a área lateral do cone pequeno
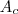
.
Considere o cone aberto e planificado, conforme a figura:
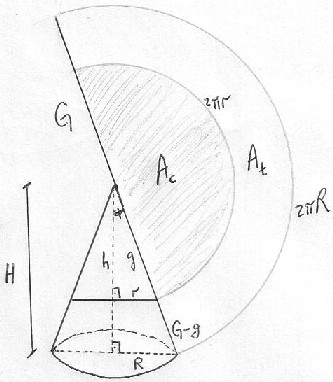
- cone_area_lateral.jpg (31.45 KiB) Exibido 17679 vezes
Calcular a área lateral do cone pequeno é equivalente a calcular a área do setor circular
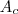
.
E
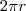
é a medida do arco determinado pelo círculo da base de raio

.
E
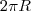
é a medida do arco determinado pelo círculo da base de raio
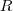
.
Fazendo uma regra de três relacionando área com arco:


A área do tronco
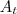
obtemos por diferença:
Sendo
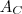
a área do cone grande, a área que procuramos é
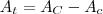
Para
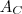
fazemos um processo análogo ao anterior e obtemos

Então
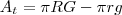
Conforme o enunciado, queremos que

, logo
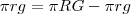

(chegamos àquela conclusão)

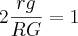
(achei mais imediato utilizar aqui a conseqüência dos triângulos semelhantes)

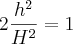

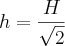

Entendendo este processo, não precisamos "alocar memória" para a "fórmula" da área lateral de um cone, pois podemos obtê-la rapidamente.
Até mais!
 e raio da base
e raio da base  é cortado por um plano paralelo à base. Calcular a altura do cone parcial assim determinado, de modo que a sua superfície lateral seja equivalente à superfície lateral do tronco de cone assim obtido.
é cortado por um plano paralelo à base. Calcular a altura do cone parcial assim determinado, de modo que a sua superfície lateral seja equivalente à superfície lateral do tronco de cone assim obtido.![\frac{h\,\sqrt[]{2}}{2} \frac{h\,\sqrt[]{2}}{2}](/latexrender/pictures/5c41e842637dcdcf786b81df6f420907.png)
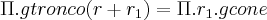
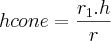
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)


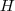 e raio da base
e raio da base 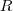 é cortado por um plano paralelo à base. Calcular a altura do cone parcial assim determinado, de modo que a sua superfície lateral seja equivalente à superfície lateral do tronco de cone assim obtido.
é cortado por um plano paralelo à base. Calcular a altura do cone parcial assim determinado, de modo que a sua superfície lateral seja equivalente à superfície lateral do tronco de cone assim obtido.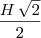
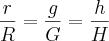


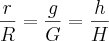 ,
,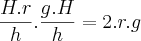
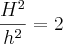
![h=\frac{H\,\sqrt[]{2}}{2} h=\frac{H\,\sqrt[]{2}}{2}](/latexrender/pictures/cb75e3fa9e6a1dd154c86a70ad6ac0da.png)
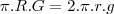
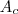 .
.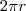 é a medida do arco determinado pelo círculo da base de raio
é a medida do arco determinado pelo círculo da base de raio 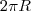 é a medida do arco determinado pelo círculo da base de raio
é a medida do arco determinado pelo círculo da base de raio 

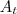 obtemos por diferença:
obtemos por diferença: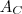 a área do cone grande, a área que procuramos é
a área do cone grande, a área que procuramos é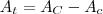

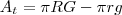
 , logo
, logo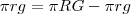
 (chegamos àquela conclusão)
(chegamos àquela conclusão)
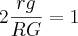 (achei mais imediato utilizar aqui a conseqüência dos triângulos semelhantes)
(achei mais imediato utilizar aqui a conseqüência dos triângulos semelhantes)
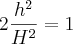

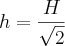

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.