 por DdSzK » Dom Ago 25, 2013 20:35
por DdSzK » Dom Ago 25, 2013 20:35
Se
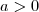
então a reta
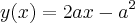
intercepta a parábola
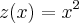
Escolher uma resposta.
a) em nenhum ponto.
b) depende do valor de a.
c) ortogonalmente.
d) em dois pontos distintos.
e) em exatamente um ponto.
-
DdSzK
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Ago 25, 2013 20:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 02:57
por Russman » Seg Ago 26, 2013 02:57
Só calcular para qual

que

. Isto é, para qual

que
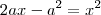
.
basta resolver a equação.
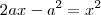
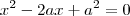
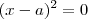

.
Logo a reta intercepta a parábola em um único ponto. Isto é, a reta é tangente a parábola em

. Note que isto faz sentido, pois a derivada de
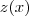
é
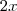
. Assim, uma reta tangente a
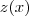
em
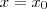
e da forma
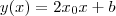
onde
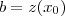
pois
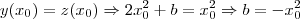
. Como

, então
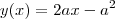
.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DdSzK » Seg Ago 26, 2013 14:08
por DdSzK » Seg Ago 26, 2013 14:08
Opa!
Vlw pela resolução, cara!
Até pensei nisso mas nao sabia o que fazer com o resultado... Hehe
Obrigado novamente

-
DdSzK
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Ago 25, 2013 20:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12991 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10972 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15112 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5030 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4794 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
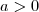 então a reta
então a reta 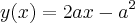 intercepta a parábola
intercepta a parábola 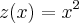

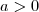 então a reta
então a reta 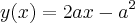 intercepta a parábola
intercepta a parábola 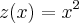

 que
que  . Isto é, para qual
. Isto é, para qual  que
que 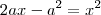 .
.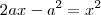
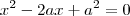
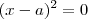
 .
. . Note que isto faz sentido, pois a derivada de
. Note que isto faz sentido, pois a derivada de 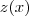 é
é 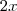 . Assim, uma reta tangente a
. Assim, uma reta tangente a 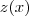 em
em 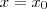 e da forma
e da forma 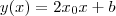 onde
onde 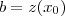 pois
pois 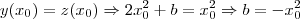 . Como
. Como  , então
, então 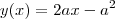 .
.




 , avisa que eu resolvo.
, avisa que eu resolvo.

