 por Cleyson007 » Sex Ago 23, 2013 00:29
por Cleyson007 » Sex Ago 23, 2013 00:29
Boa noite!
Considere o grupo aditivo
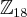
e
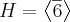
e
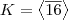
. Mostre que

é um subgrupo cíclico de
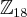
gerado por
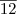
.
Se alguém souber, agradeço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Renato_RJ » Sex Ago 23, 2013 01:47
por Renato_RJ » Sex Ago 23, 2013 01:47
Sabe dizer se H e K são subgrupos de
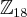
???
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Renato_RJ » Sex Ago 23, 2013 14:27
por Renato_RJ » Sex Ago 23, 2013 14:27
Cleyson007 escreveu:Boa noite!
Considere o grupo aditivo
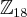
e
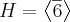
e
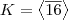
. Mostre que

é um subgrupo cíclico de
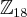
gerado por
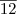
.
Se alguém souber, agradeço.
Se H e K forem subgrupos, então

é um subgrupo (se precisar, é fácil demonstrar). O subgrupo H é formado por

e o subgrupo K é formado por
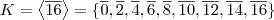
portanto a interseção
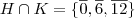
o que é um subgrupo (como afirmei anteriormente) cíclico (veja que, aplicando sucessivamente a operação do grupo a classe 12 as classes do subgrupo

se repetirão) gerado por
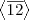
.
Editado pela última vez por
Renato_RJ em Sex Ago 23, 2013 22:41, em um total de 2 vezes.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Cleyson007 » Sex Ago 23, 2013 16:28
por Cleyson007 » Sex Ago 23, 2013 16:28
Renato, se não for incomodo demonstre por favor que H ? K é um subgrupo.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Renato_RJ » Sex Ago 23, 2013 22:34
por Renato_RJ » Sex Ago 23, 2013 22:34
Cleyson007 escreveu:Renato, se não for incomodo demonstre por favor que H ? K é um subgrupo.
Supondo H e K sejam subgrupo de
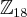
com a operação de soma, então:
1 -
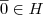
e
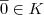
por definição, logo
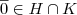
2 - Sejam

. Como H é subgrupo de
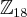
e
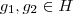
então
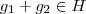
. Analogamente para K, então
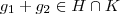
.
3 - Seja
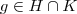
, como H é subgrupo então existe
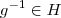
. Analogamente para K, então
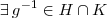
Logo

é subgrupo de
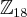
.
Qualquer coisa, posta aí..
Abraços.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão dificil.
por natanskt » Seg Dez 13, 2010 18:20
- 1 Respostas
- 2455 Exibições
- Última mensagem por Molina

Sáb Dez 25, 2010 20:28
Binômio de Newton
-
- Questão dificil
por cortelettirlz » Qua Set 07, 2011 15:32
- 1 Respostas
- 1611 Exibições
- Última mensagem por MarceloFantini

Dom Set 11, 2011 19:43
Sistemas de Equações
-
- Questão Difícil
por Bira » Dom Ago 12, 2012 17:55
- 0 Respostas
- 1330 Exibições
- Última mensagem por Bira

Dom Ago 12, 2012 17:55
Probabilidade
-
- Retas questão dificil
por o_andrade » Qui Jul 28, 2011 22:06
- 1 Respostas
- 1491 Exibições
- Última mensagem por o_andrade

Qui Jul 28, 2011 23:04
Geometria Analítica
-
- Dificil questao de probabilidade
por bmachado » Seg Jun 11, 2012 16:29
- 2 Respostas
- 3586 Exibições
- Última mensagem por bmachado

Qua Jun 13, 2012 22:03
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
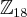 e
e 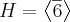 e
e 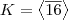 . Mostre que
. Mostre que  é um subgrupo cíclico de
é um subgrupo cíclico de 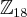 gerado por
gerado por 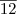 .
.
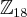 e
e 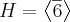 e
e 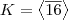 . Mostre que
. Mostre que  é um subgrupo cíclico de
é um subgrupo cíclico de 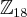 gerado por
gerado por 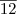 .
.
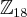 ???
???
e
e
. Mostre que
é um subgrupo cíclico de
gerado por
.
 é um subgrupo (se precisar, é fácil demonstrar). O subgrupo H é formado por
é um subgrupo (se precisar, é fácil demonstrar). O subgrupo H é formado por  e o subgrupo K é formado por
e o subgrupo K é formado por 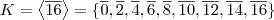 portanto a interseção
portanto a interseção 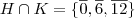 o que é um subgrupo (como afirmei anteriormente) cíclico (veja que, aplicando sucessivamente a operação do grupo a classe 12 as classes do subgrupo
o que é um subgrupo (como afirmei anteriormente) cíclico (veja que, aplicando sucessivamente a operação do grupo a classe 12 as classes do subgrupo  se repetirão) gerado por
se repetirão) gerado por 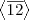 .
.

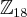 com a operação de soma, então:
com a operação de soma, então: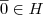 e
e 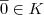 por definição, logo
por definição, logo 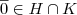
 . Como H é subgrupo de
. Como H é subgrupo de 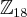 e
e 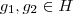 então
então 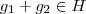 . Analogamente para K, então
. Analogamente para K, então 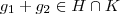 .
.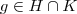 , como H é subgrupo então existe
, como H é subgrupo então existe 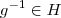 . Analogamente para K, então
. Analogamente para K, então 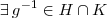
 é subgrupo de
é subgrupo de 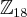 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

