(Fatec 99) O dono de uma rede hoteleira verificou que em certa região tem havido um decréscimo no número de hóspedes em seus pacotes promocionais, e esse decréscimo tem sido linear em relação ao tempo. Em 1982, a média foi de 600 pessoas por semana, enquanto que em 1990 a média semanal foi de 432.
Dessa forma, o número médio de hóspedes por semana,
a) em 1995, foi de 322.
b) em 1994, foi de 345.
c) em 1993, foi de 370.
d) em 1992, foi de 392.
e) em 1991, foi de 411.
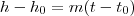, onde 
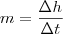você vai achar que 
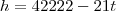, então é só ir substituindo os valores dos anos no lugar do t que você vai achar o h e verificar se é verdade.
então se tem que h=327, logo essa alternataiva é falsa.
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.