 por geobson » Sáb Ago 10, 2013 15:08
por geobson » Sáb Ago 10, 2013 15:08
ja tentei ,mas não consegui resolver este problema de somatória .foi retirado do livro geometria plana simples assim de wanderson coelho cardoso ,no capítulo de triângulos retângulos.deve ter algo a ver com o teorema de pitágoras...
por favor quem souber resolva ou pelo menos alguma sugestão
desde ja fico grato...
para todo n positivo, seja
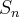
ovalor mínimo da soma :

![\sqrt[]{(k-1)²+ak²} \sqrt[]{(k-1)²+ak²}](/latexrender/pictures/801f7567ac1c51d466bf588bff446099.png)
, onde
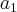
,
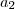
, ...,

são numeros reais positivos cuja soma é igual a 17. sabendo que existe um único número inteiro positivo n para o qual
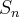
é também um número inteiro , o valor de n é igual a :
a)10
b)12
c)15
d)16
e)17
não sei explicar ,mas o  dentro da raiz (a maiúsculo não existe na expressao )!!!!!!!!!!!!!! a expressão (2k-1)²+ak² existe mas o  não existe
-
geobson
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Ago 03, 2013 22:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Dom Ago 11, 2013 18:52
por young_jedi » Dom Ago 11, 2013 18:52
pensei no seguinte se considerarmos triângulos retângulos todos semelhantes com catetos dados por

e
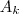
então a hipotenusa de cada triangulo sera

sendo assim o somatorio é igual ao a soma das hipotenusas desses triangulos
como todos os triângulos são semelhantes então existe um triângulo semelhante aos demais em que seus catetos são dados pela soma dos catetos de todos esses trianulos e a hipotenusa é a soma de todas as hipotenusas de todos esses triângulos, sabemos que a soma dos catetos

portanto um dos catetos desse triangulo é 17 e o outro é dado pela soma



então o outro cateto mede
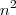
então a hipotenusa que é igual ao somatório que queremos encontrar é dada por

temos que encontrar um valor para n para o qual essa raiz de um valor exato
dos valores dados ai nas respostas o que satisfaz é n=12

não sei se tem outra forma de se resolver, vou continuar pensando qualquer evolução eu posto aqui
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Dom Ago 11, 2013 21:19
por e8group » Dom Ago 11, 2013 21:19
Muito interessante a solução acima .Só gostaria de acrescentar mais uma ideia de forma a não usarmos as alternativas para calcular o valor de

.
Conforme young jedi propôs sendo todos triângulos retângulos(nomeando eles de

) de catetos

e hipotenusa

(que vamos designar por

) semelhantes . Evidenciando a constante de proporcionalidade dos lados dos triângulos

concluímos que o triângulo retângulo de catetos

e hipotenusa

é semelhante a todos triângulos retângulos

. Agora notamos que a hipotenusa deste triângulo retângulo é estritamente maior que
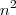
, pois ,

.
Tomemos então um

natural de modo que ,

. Elevando ao quadrado e simplificando ,

. Aqui cabe analisar se

ou

divide

.É fácil verificar que

não divide tal número . Assim , segue :

(pois caso fosse

chegaríamos em um absurdo

uma vez que

) . Daí obtemos
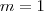
e portanto

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Dom Ago 11, 2013 23:31
por young_jedi » Dom Ago 11, 2013 23:31
excelente demonstração santhiago, valeu ai pela força !!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
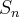 ovalor mínimo da soma :
ovalor mínimo da soma : 
![\sqrt[]{(k-1)²+ak²} \sqrt[]{(k-1)²+ak²}](/latexrender/pictures/801f7567ac1c51d466bf588bff446099.png) , onde
, onde 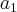 ,
, 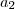 , ...,
, ...,  são numeros reais positivos cuja soma é igual a 17. sabendo que existe um único número inteiro positivo n para o qual
são numeros reais positivos cuja soma é igual a 17. sabendo que existe um único número inteiro positivo n para o qual 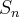 é também um número inteiro , o valor de n é igual a :
é também um número inteiro , o valor de n é igual a :

 e
e 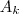

 portanto um dos catetos desse triangulo é 17 e o outro é dado pela soma
portanto um dos catetos desse triangulo é 17 e o outro é dado pela soma


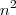 então a hipotenusa que é igual ao somatório que queremos encontrar é dada por
então a hipotenusa que é igual ao somatório que queremos encontrar é dada por


 .
. ) de catetos
) de catetos  e hipotenusa
e hipotenusa  (que vamos designar por
(que vamos designar por  ) semelhantes . Evidenciando a constante de proporcionalidade dos lados dos triângulos
) semelhantes . Evidenciando a constante de proporcionalidade dos lados dos triângulos  concluímos que o triângulo retângulo de catetos
concluímos que o triângulo retângulo de catetos  e hipotenusa
e hipotenusa  é semelhante a todos triângulos retângulos
é semelhante a todos triângulos retângulos  .
.  natural de modo que ,
natural de modo que ,  . Elevando ao quadrado e simplificando ,
. Elevando ao quadrado e simplificando ,  . Aqui cabe analisar se
. Aqui cabe analisar se  divide
divide  .É fácil verificar que
.É fácil verificar que  (pois caso fosse
(pois caso fosse  chegaríamos em um absurdo
chegaríamos em um absurdo uma vez que
uma vez que  ) . Daí obtemos
) . Daí obtemos 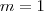 e portanto
e portanto  .
. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: