 por barbara-rabello » Seg Ago 05, 2013 19:11
por barbara-rabello » Seg Ago 05, 2013 19:11
Prove que para quaisquer conjuntos A e B temos A

B se, e somente se, para qualquer conjunto C vale
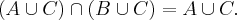
Estou com dificuldade nesta questão, posso tentar fazer por Indução? Ou talvez por Absurdo?
Valeu!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Seg Ago 05, 2013 22:45
por e8group » Seg Ago 05, 2013 22:45
Ainda não estudei teoria dos conjuntos como gostaria ,portanto talvez o que postarei apresentará erros .
Suponha
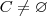
.Vamos mostar que se

,então :
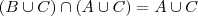
.
Dado ,

em

,segue-se que
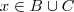 e
e 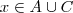
sse
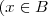 ou
ou 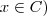 e
e 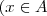 ou
ou 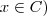
.
Desde que

,temos que
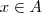 e
e 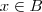
sse
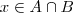
sse
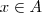
. Daí resulta ,
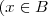 ou
ou 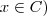 e
e 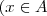 ou
ou 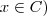
sse
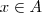 ou
ou 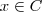
o que mostra
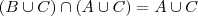
.
Reciprocamente, seja
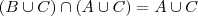
. Dado ,
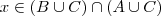
.Temos :
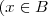 ou
ou 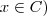 e
e 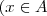 ou
ou 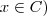
.
Por outro lado :
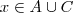
sse
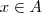
o
u 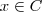
.
Logo , obtemos
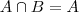
e portanto
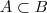
.
O caso

é obvio .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por barbara-rabello » Sex Ago 09, 2013 15:14
por barbara-rabello » Sex Ago 09, 2013 15:14
Obrigada pela ajuda! Vou tentar refazer a questão seguindo a sua lógica.
Uma dúvida, quando você continuou a explicação a partir do reciprocamente, essa parte é para o O caso

?
Pois achei meio estranha, se for.
Valeu!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por barbara-rabello » Sex Ago 09, 2013 15:25
por barbara-rabello » Sex Ago 09, 2013 15:25
Desculpa a pergunta, mas o que significa sse ?
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Sex Ago 09, 2013 22:00
por e8group » Sex Ago 09, 2013 22:00
barbara-rabello escreveu:Obrigada pela ajuda! Vou tentar refazer a questão seguindo a sua lógica.
Uma dúvida, quando você continuou a explicação a partir do reciprocamente, essa parte é para o O caso

?
Pois achei meio estranha, se for.
Valeu!
Não há de quê .A resolução a partir do reciprocamente não é para o caso

. Mas claramente quando

o resultado que foi provado (caso não contenha erros )acima também vale para este caso. Pois ,
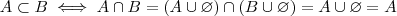
.
barbara-rabello escreveu:Desculpa a pergunta, mas o que significa sse ?
" Se e somente se " ou " se e só se " (abreviadamente ,
sse )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por barbara-rabello » Sex Ago 09, 2013 22:13
por barbara-rabello » Sex Ago 09, 2013 22:13
Muito obrigada mesmo pela ajuda!
Consegui entender sua lógica. Bem que eu achei que estava estranho se fosse para o segundo caso.
Mas uma vez, obrigada!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6390 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3674 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2894 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2286 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4418 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 B se, e somente se, para qualquer conjunto C vale
B se, e somente se, para qualquer conjunto C vale 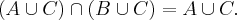

 B se, e somente se, para qualquer conjunto C vale
B se, e somente se, para qualquer conjunto C vale 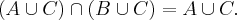

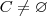 .Vamos mostar que se
.Vamos mostar que se  ,então :
,então :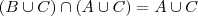 .
. em
em  ,segue-se que
,segue-se que 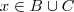 e
e 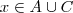 sse
sse 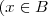 ou
ou 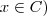 e
e 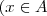 ou
ou 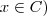 .
.  ,temos que
,temos que 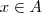 e
e 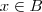 sse
sse 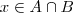 sse
sse 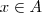 . Daí resulta ,
. Daí resulta , 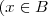 ou
ou 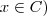 e
e 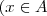 ou
ou 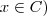 sse
sse 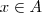 ou
ou 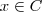 o que mostra
o que mostra 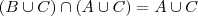 .
. 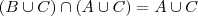 . Dado ,
. Dado , 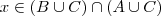 .Temos :
.Temos : 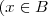 ou
ou 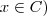 e
e 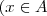 ou
ou 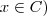 .
.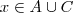 sse
sse 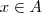 ou
ou 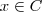 .
.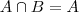 e portanto
e portanto 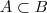 .
. é obvio .
é obvio .
 ?
?

?
 . Mas claramente quando
. Mas claramente quando  o resultado que foi provado (caso não contenha erros )acima também vale para este caso. Pois ,
o resultado que foi provado (caso não contenha erros )acima também vale para este caso. Pois , 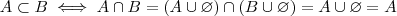 .
.

