 por Luiz Felipe » Ter Jun 05, 2012 21:32
por Luiz Felipe » Ter Jun 05, 2012 21:32
Questão : Um marceneiro cortou uma tabua retangular de 75 cm de comprimento por 20 cm de largura , separando-a em dois trapezios congruentes.Sabendo-se que o comprimento do corte foi de 25 cm, calcule a medida da base menor de um dos trapézios.
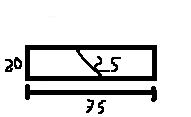
- FIGURA
- edaasaas.JPG (3.7 KiB) Exibido 2820 vezes
RESP: 30CMTentativa : eu peguei a base menor do trapezio e formei um triângulo retangulo, (largura-cateto oposto 20cm, corte-hipotenusa 25cm, base menor "x"), tentei usa um Pitagoras, mas não bateu com a resposta, segue a resolução :
![{a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15 {a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15](/latexrender/pictures/749f99f2c20ad8724eb0f59b9b45935b.png)
Agradeço a atenção, o tempo e a ajuda de quem se dispor, obrigado.
-
Luiz Felipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 13, 2012 15:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciências Biologicas
- Andamento: cursando
 por MarceloFantini » Qua Jun 06, 2012 02:28
por MarceloFantini » Qua Jun 06, 2012 02:28
Sua resolução está incompleta. Veja a figura anexada para entender melhor. O que você fez foi encontrar o tamanho do cateto restante. Agora, sabemos que tudo vale 15, logo este pedaço debaixo vale

. Como temos um retângulo, o lado de cima é igual ao lado debaixo, daí
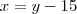
, e também sabemos
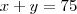
. Isolando

em função de

, segue
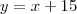
e
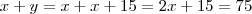
, finalmente

.
- Anexos
-
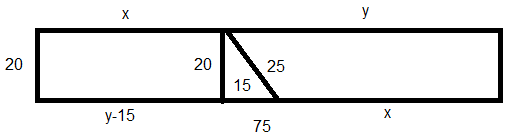
- Desenho auxiliar
- geometria.png (3.3 KiB) Exibido 2816 vezes
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Pandaludo » Ter Ago 06, 2013 17:31
por Pandaludo » Ter Ago 06, 2013 17:31
Professor, MarceloFantini , por que o senhor disse que aqueles lados eram iguais, se no texto isto não estava explícito? Refiro-me ao x. Obrigada.
-
Pandaludo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Ago 06, 2013 17:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em geometria plana
 por tadeutato » Seg Abr 25, 2011 11:26
por tadeutato » Seg Abr 25, 2011 11:26
- 2 Respostas
- 1669 Exibições
- Última mensagem por SidneySantos

Seg Abr 25, 2011 22:33
Geometria Plana
-
- Duvida - Geometria Plana 2
 por Luiz Felipe » Ter Jun 05, 2012 22:27
por Luiz Felipe » Ter Jun 05, 2012 22:27
- 1 Respostas
- 1133 Exibições
- Última mensagem por MarceloFantini

Qua Jun 06, 2012 02:38
Geometria Plana
-
- Duvida - Geometria Plana 3
 por Luiz Felipe » Ter Jun 05, 2012 22:48
por Luiz Felipe » Ter Jun 05, 2012 22:48
- 1 Respostas
- 7833 Exibições
- Última mensagem por MarceloFantini

Qua Jun 06, 2012 02:45
Geometria Plana
-
- [Geometria Plana] Duvida
 por Micael » Qui Mar 14, 2013 17:57
por Micael » Qui Mar 14, 2013 17:57
- 1 Respostas
- 1095 Exibições
- Última mensagem por timoteo

Qui Mar 14, 2013 18:34
Geometria Plana
-
- [Geometria Plana] DÚVIDA
 por Micael » Seg Mai 13, 2013 19:38
por Micael » Seg Mai 13, 2013 19:38
- 1 Respostas
- 2733 Exibições
- Última mensagem por Molina

Seg Mai 13, 2013 23:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15 {a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15](/latexrender/pictures/749f99f2c20ad8724eb0f59b9b45935b.png)


 . Como temos um retângulo, o lado de cima é igual ao lado debaixo, daí
. Como temos um retângulo, o lado de cima é igual ao lado debaixo, daí 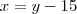 , e também sabemos
, e também sabemos 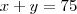 . Isolando
. Isolando  em função de
em função de  , segue
, segue 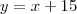 e
e 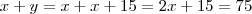 , finalmente
, finalmente  .
.

