 por Jeks_Osodrac » Ter Jul 30, 2013 19:19
por Jeks_Osodrac » Ter Jul 30, 2013 19:19
-
Jeks_Osodrac
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 30, 2013 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletrônica
- Andamento: formado
 por Russman » Qua Jul 31, 2013 01:52
por Russman » Qua Jul 31, 2013 01:52
Nós aqui do fórum achamos mais producente que você ao expor suas dúvidas exponha junto com elas a sua tentativa de resolução para que possamos te ajudar a resolver a questão ao invés de resolvê-la por você. Mas como estou com tempo agora eu vou deixar a solução aqui. Mas procure, futuramente, não repetir esse comportamento para o próprio bem do seu aprendizado.
25)
O exercício pede que você calcule a taxa de variação (TDV) da área do triângulo com relação a variação do catetos. Assim, a primeira coisa a ser feita é expressar a área em função destes, certo?
Como o triângulo é retângulo a sua área é dada pela metade do produto dos catetos. Sejam
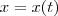
e
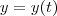
os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por
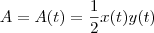
de modo que
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)]](/latexrender/pictures/1a34075169e113ffc583d801742964d0.png)
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ]](/latexrender/pictures/cdeb48e51d261a2ada33e8fa596743a2.png)
e , portanto,
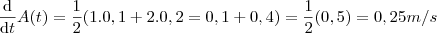
.
26)
Para resolver esta basta fazer exatamente o que fiz na questão anterior. Expresse o volume do cone em função da altura e do raio de base, derive e voilà.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jeks_Osodrac » Qua Jul 31, 2013 12:46
por Jeks_Osodrac » Qua Jul 31, 2013 12:46
O que seria esse 1/2 ??
Ah entendi, Obrigada!
Mas não é triângulo rsrs :p
-
Jeks_Osodrac
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 30, 2013 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletrônica
- Andamento: formado
 por Russman » Qua Jul 31, 2013 18:03
por Russman » Qua Jul 31, 2013 18:03
Eu li triângulo retângulo ao invés de retângulo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Taxa de variação
por Aliocha Karamazov » Sáb Nov 26, 2011 18:40
- 3 Respostas
- 8075 Exibições
- Última mensagem por MarceloFantini

Dom Nov 27, 2011 01:57
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Taxa de Variação
por Vanny » Dom Set 30, 2012 20:58
- 0 Respostas
- 3113 Exibições
- Última mensagem por Vanny

Dom Set 30, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada como Taxa de Variação
por Ronaldobb » Sex Set 21, 2012 20:29
- 3 Respostas
- 2269 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 00:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Taxa de variação - velocidade
por emanes » Qua Out 17, 2012 11:10
- 1 Respostas
- 3934 Exibições
- Última mensagem por young_jedi

Qua Out 17, 2012 11:50
Cálculo: Limites, Derivadas e Integrais
-
- Derivada taxa de variação - HELP Por favor
por vivik » Ter Mai 15, 2018 16:47
- 0 Respostas
- 2961 Exibições
- Última mensagem por vivik

Ter Mai 15, 2018 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



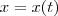 e
e 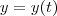 os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por
os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por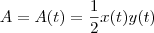
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)]](/latexrender/pictures/1a34075169e113ffc583d801742964d0.png)
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ]](/latexrender/pictures/cdeb48e51d261a2ada33e8fa596743a2.png)
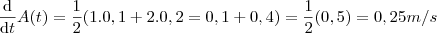 .
.

