Pessoal, alguém me ajuda a entender a questão abaixo:
CESPE/UnB – SERPRO/2013 - Considerando que x,y e z sejam números naturais tais que
x+y=z;que X seja a proposição “x é ímpar”; que Y seja a proposição
“y é par”; e que Z seja a proposição “z é ímpar”, julgue os seguintes
itens.
A proposição X^Z->Y é verdadeira.
A proposição Y->X^Z é verdadeira.


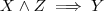 significa:
significa: é ímpar e
é ímpar e  é ímpar implica que
é ímpar implica que  é par.
é par.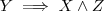 significa:
significa: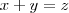 , com
, com 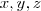 naturais, terás que verificar se essas sentenças são verdadeiras ou falsas.
naturais, terás que verificar se essas sentenças são verdadeiras ou falsas.
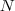 par pode ser escrito da forma
par pode ser escrito da forma  onde
onde  é um número natural, ao passo de que todo
é um número natural, ao passo de que todo 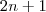 .
. e
e 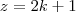 ,
,  naturais, de forma que
naturais, de forma que 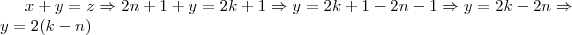
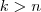 , então se
, então se  ( onde
( onde 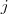 é um número natural) e , portanto,
é um número natural) e , portanto,  ( um par) , então
( um par) , então
 tem de ser par e isso só ocorre se ambos forem ímpares ou ambos forem pares.
tem de ser par e isso só ocorre se ambos forem ímpares ou ambos forem pares.

 .
.
 :
: