 por bakunin95 » Sex Jul 26, 2013 21:36
por bakunin95 » Sex Jul 26, 2013 21:36
Os gráficos das funções
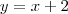
e
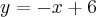
definem, com os eixos, no primeiro quadrante, um quadrilátero de área:
a)12
b)16
c)10
d)8
e)14
eu fiz a conta e o resultado deu 8, mas a figura foi formada no 2º quadrante, e não no primeiro, se alguém puder me ajudar eu agradeço
-
bakunin95
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mai 17, 2013 00:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fabriel » Sáb Jul 27, 2013 00:13
por fabriel » Sáb Jul 27, 2013 00:13
Você tem a resposta?
Eu cheguei na letra e) 14 u.a
é só desenhar as retas certinhos no plano cartesiano.
Depois você calcula por partes as figuras que podem serem formadas.... um Triangulo e um trapézio por exemplo.
Uma dica é iguala as funções x+2=-x+6. Você vai achar que x=2, que é o ponto de intersecção das retas.
É só desenhar que ai vc verá a medida das figuras, tenta ai.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por bakunin95 » Seg Jul 29, 2013 04:47
por bakunin95 » Seg Jul 29, 2013 04:47
A resposta está certa e depois de tentar novamente eu acertei. Meu problema estava pq as linhas estavam formando a figura no 2º quadrante, pq eu não tinha me atentado para o sinal, que significava a degressividade da reta da função. muito obg cara.
-
bakunin95
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mai 17, 2013 00:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Mackenzie) função 1° grau
por my2009 » Seg Dez 06, 2010 17:35
- 3 Respostas
- 11605 Exibições
- Última mensagem por my2009

Seg Dez 06, 2010 23:17
Funções
-
- Função de Primeiro Grau
por Najyh » Seg Mai 03, 2010 23:22
- 3 Respostas
- 5041 Exibições
- Última mensagem por MarceloFantini

Ter Mai 04, 2010 22:41
Funções
-
- função do primeiro grau
por Abelardo » Qua Abr 27, 2011 19:35
- 2 Respostas
- 4194 Exibições
- Última mensagem por Abelardo

Qui Abr 28, 2011 11:08
Álgebra Elementar
-
- Função do Primeiro Grau
por Rafael16 » Sex Jan 11, 2013 21:20
- 2 Respostas
- 4114 Exibições
- Última mensagem por DanielFerreira

Sex Jan 11, 2013 22:27
Funções
-
- Função do primeiro Grau.
por jhonathanrsy » Ter Abr 07, 2015 11:48
- 0 Respostas
- 3570 Exibições
- Última mensagem por jhonathanrsy

Ter Abr 07, 2015 11:48
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
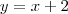 e
e 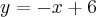 definem, com os eixos, no primeiro quadrante, um quadrilátero de área:
definem, com os eixos, no primeiro quadrante, um quadrilátero de área: 

