 por Jhonata » Sex Jul 19, 2013 19:44
por Jhonata » Sex Jul 19, 2013 19:44
Eu conheço a aplicação dos mínimos quadrados, no entanto, não estou conseguindo resolver a seguinte questão:
A reta que melhor ajusta os dados da tabela:
[x --- y]
[1 -7]
[2 8]
[3 -13]
no sentido dos mínimos quadrados é

. Usando este fato, determine a projeção ortogonal do vetor

) sobre

.
Agradeço a todos pela atenção e ficarei mais grato ainda aquele que puder me ajudar.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Sáb Jul 20, 2013 17:12
por MateusL » Sáb Jul 20, 2013 17:12
Oi Jhonata.
O que simboliza <(1,2,3),(1,1,1)> ? É o produto escalar de dois vetores? Se for, a questão não tem sentido...
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Sáb Jul 20, 2013 17:30
por Jhonata » Sáb Jul 20, 2013 17:30
MateusL escreveu:Oi Jhonata.
O que simboliza <(1,2,3),(1,1,1)> ? É o produto escalar de dois vetores? Se for, a questão não tem sentido...
Abraço!
Opa, perdoe-me ! Eu havia esquecido esse detalhe. É que minha apostila(um pouco louca rsrs) utiliza duas notações.
No caso, seria o espaço gerado pelos vetores, ou melhor: span{(1,2,3),(1,1,1)}.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Sáb Jul 20, 2013 18:34
por MateusL » Sáb Jul 20, 2013 18:34
Sem problemas!
Realmente não sei muito dessa parte, mas pesquisando aqui achei este teorema:
Se

é uma matriz

com vetores-coluna linearmente independentes, então para cada matriz

de tamanho

, o sistema linear

tem uma única solução de mínimos quadrados. Esta solução é dada por:

Além disso, se

é o espaço-coluna de

, então a projeção ortogonal de

em

é:

Vetor-coluna de

é um vetor formado pelos elementos de uma coluna de

Espaço-coluna de

é o subespaço gerado pelas colunas de

.
Espero que isso ajude.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Sáb Jul 20, 2013 18:53
por Jhonata » Sáb Jul 20, 2013 18:53
Eu conheço o Teorema e é este mesmo que estou tentando aplicar nessa questão, mas não está dando certo.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Sáb Jul 20, 2013 18:53
por Jhonata » Sáb Jul 20, 2013 18:53
Eu conheço o Teorema e é este mesmo que estou tentando aplicar nessa questão, mas não está dando certo.
De qualquer forma, muito obrigado!
Desculpa o spam, ocorreu um problema com minha internet.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Dom Jul 21, 2013 00:41
por MateusL » Dom Jul 21, 2013 00:41
Vou ver se consigo.
Queremos encontrar

e

tal que

para todos os valores de

na tabela.
Ou seja, queremos resolver o seguinte sistema:

Seja

,

e

.
Então podemos representar o sistema por

(não confundir este

com o

do enunciado).
Este não é um sistema linear compatível, mas sabemos que a reta que melhor ajusta os dados no sentido dos mínimos quadrados é:
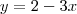
Então

e

, ou seja, a solução pelo método dos mínimos quadrados é

.
É claro que usando estes valores para

, não encontrarás exatamente os valores para

, mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de

da tabela e o valor de

obtido utilizando este valor de

.
Seja

o subespaço formado pelos vetores-coluna de

.
Queremos encontrar a projeção ortogonal de

sobre

.
Pelo teorema que já postei acima:
... se

é o espaço-coluna de

, então a projeção ortogonal de

em

é:

Então:

Acredito que seja isso.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Dom Jul 21, 2013 10:49
por Jhonata » Dom Jul 21, 2013 10:49
É isso mesmo! Muito obrigado! Salvou meus estudos. rsrs
Estava quebrando a cabeça com essa questão até agora, mas era tão simples que até me senti estúpido.
Novamente, muito obrigado!
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Projeção Ortogonal
por Balanar » Dom Out 24, 2010 18:19
- 0 Respostas
- 2096 Exibições
- Última mensagem por Balanar

Dom Out 24, 2010 18:19
Geometria Plana
-
- projeção ortogonal {vetores}
 por Danilo » Ter Nov 06, 2012 19:57
por Danilo » Ter Nov 06, 2012 19:57
- 3 Respostas
- 5300 Exibições
- Última mensagem por LuizAquino

Qua Nov 07, 2012 16:16
Geometria Analítica
-
- Planos paralelos e projeção ortogonal
por dandara » Seg Dez 29, 2014 10:18
- 1 Respostas
- 2295 Exibições
- Última mensagem por adauto martins

Sex Jan 02, 2015 14:49
Geometria Espacial
-
- [operador linear] calcular projeção ortogonal
por Ge_dutra » Sáb Mar 16, 2013 19:42
- 0 Respostas
- 1560 Exibições
- Última mensagem por Ge_dutra

Sáb Mar 16, 2013 19:42
Álgebra Linear
-
- Problema de mínimos quadrados
por brunozi » Ter Set 29, 2009 10:54
- 0 Respostas
- 1744 Exibições
- Última mensagem por brunozi

Ter Set 29, 2009 10:54
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Usando este fato, determine a projeção ortogonal do vetor
. Usando este fato, determine a projeção ortogonal do vetor  ) sobre
) sobre  .
.

 é uma matriz
é uma matriz  com vetores-coluna linearmente independentes, então para cada matriz
com vetores-coluna linearmente independentes, então para cada matriz  de tamanho
de tamanho  , o sistema linear
, o sistema linear  tem uma única solução de mínimos quadrados. Esta solução é dada por:
tem uma única solução de mínimos quadrados. Esta solução é dada por:
 é o espaço-coluna de
é o espaço-coluna de 
 e
e  tal que
tal que  para todos os valores de
para todos os valores de  na tabela.
na tabela.
 ,
,  e
e  .
.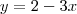
 e
e  , ou seja, a solução pelo método dos mínimos quadrados é
, ou seja, a solução pelo método dos mínimos quadrados é  .
. , mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de
, mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de 





