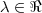 para que o seguinte subespaço de
para que o seguinte subespaço de 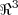 tenha dimensão 1.
tenha dimensão 1.

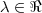 para que o seguinte subespaço de
para que o seguinte subespaço de 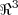 tenha dimensão 1.
tenha dimensão 1.

 são três vetores colineares.
são três vetores colineares. e
e  são múltiplos de
são múltiplos de  .
.
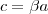
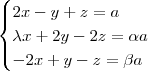
 e subtraindo a primeira da segunda obteremos:
e subtraindo a primeira da segunda obteremos:
 e
e  , para que a equação acima seja verdadeira devemos ter:
, para que a equação acima seja verdadeira devemos ter:
 e, finalmente,
e, finalmente,  .
. .
. . Agora o valor está certo!
. Agora o valor está certo!
 a matriz que está multiplicando a matriz coluna
a matriz que está multiplicando a matriz coluna  . Observando que a última linha da matriz
. Observando que a última linha da matriz  é múltipla da primeira ,segue
é múltipla da primeira ,segue  é singular
é singular  é um sistema compatível e indeterminado .Em particular , se
é um sistema compatível e indeterminado .Em particular , se  , então o sistema linear homogêneo
, então o sistema linear homogêneo  admite outras soluções além da trivial (1) . Agora , seja
admite outras soluções além da trivial (1) . Agora , seja  .Então ,
.Então ,  . Por outro lado ,
. Por outro lado ,  .
. , por (1)
, por (1)  ,daí resulta
,daí resulta  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)