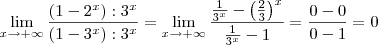por Pessoa Estranha » Ter Jul 16, 2013 17:15
por Pessoa Estranha » Ter Jul 16, 2013 17:15
Boa Tarde. Gostaria que alguém me ajudasse a resolver dois limites, tais que tentei solucionar várias vezes, mas não consegui. Aqui vão os limites:
lim (2^x - 3^x), quando x->

lim ((1 - 2^x)/(1 - 3^x)), quando x->

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Como tentei resolver:
lim (2^x - 3^x), quando x->

= lim (2^x), quando x->

, - lim (3^x), quando x->

=

-

(Mas este resultado é uma indeterminação. Tentei também de outras maneiras, mas todas sempre chegavam numa indeterminação).
lim ((1 - 2^x)/(1 - 3^x)), quando x->

= lim (1 - 2^x),quando x->

/ lim (1 - 3^x), quando x->

(indeterminação).
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Ter Jul 16, 2013 18:02
por Russman » Ter Jul 16, 2013 18:02
No primeiro caso, note que
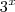
se aproxima de infinito mais rapidamente que
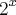
, pois

. Assim, o primeiro limite vai para

.
No segundo caso, o denominador fica sempre ''mais negativo'' que o numerador. Consequentemente, o denominador fica sempre , em módulo, maior que o numerado. Assim, esse limite tende a zero.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizAquino » Qua Jul 17, 2013 09:12
por LuizAquino » Qua Jul 17, 2013 09:12
Pessoa Estranha escreveu:Boa Tarde. Gostaria que alguém me ajudasse a resolver dois limites, tais que tentei solucionar várias vezes, mas não consegui. Aqui vão os limites:
lim (2^x - 3^x), quando x->

lim ((1 - 2^x)/(1 - 3^x)), quando x->

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Como tentei resolver:
lim (2^x - 3^x), quando x->

= lim (2^x), quando x->

, - lim (3^x), quando x->

=

-

(Mas este resultado é uma indeterminação. Tentei também de outras maneiras, mas todas sempre chegavam numa indeterminação).
lim ((1 - 2^x)/(1 - 3^x)), quando x->

= lim (1 - 2^x),quando x->

/ lim (1 - 3^x), quando x->

(indeterminação).
Russman escreveu:No primeiro caso, note que
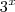
se aproxima de infinito mais rapidamente que
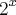
, pois

. Assim, o primeiro limite vai para

.
No segundo caso, o denominador fica sempre ''mais negativo'' que o numerador. Consequentemente, o denominador fica sempre , em módulo, maior que o numerado. Assim, esse limite tende a zero.
Eu vou apresentar uma outra maneira de resolver. Desta vez uma maneira algébrica.
Como você mesmo já notou, o primeiro limite é uma indeterminação do tipo

. A estratégia é tentar reescrevê-lo de tal modo que não haja mais indeterminação. Para isso, note que colocando
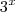
em evidência obtemos:
![\lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty \lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty](/latexrender/pictures/a27ac0e1686c0171f437b9e3073528b0.png)
Já no segundo limite, temos uma indeterminação do tipo
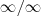
. Para remover esta indeterminação, note que dividindo o numerador e o denominador por
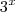
obtemos:
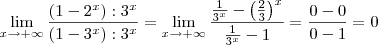 Observação
ObservaçãoEu sugiro que você estude o LaTeX para digitar os textos matemáticos de modo mais adequado. Vide o tópico
DICA: Escrevendo Fórmulas com LaTeX via BBCode.
Tenha certeza que o LaTeX será útil para você não só aqui nas mensagens do fórum, mas em toda a sua vida acadêmica e profissional.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3708 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- Ajuda para Calcular uma Integral Gaussiana
por Luthius » Qui Jul 12, 2018 09:22
- 0 Respostas
- 4360 Exibições
- Última mensagem por Luthius

Qui Jul 12, 2018 09:22
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para Limites
por Optikool » Seg Jan 07, 2013 12:04
- 1 Respostas
- 1763 Exibições
- Última mensagem por e8group

Seg Jan 07, 2013 23:40
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para Limites Parte 2
por Optikool » Seg Jan 07, 2013 12:11
- 1 Respostas
- 1785 Exibições
- Última mensagem por e8group

Seg Jan 07, 2013 21:48
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] AJUDA PARA RESOLVER A MEDIDA DE EFICIÊNCIA !!
por davidvmatos » Qui Abr 03, 2014 00:29
- 1 Respostas
- 1958 Exibições
- Última mensagem por fff

Seg Abr 07, 2014 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 = lim (2^x), quando x->
= lim (2^x), quando x-> , - lim (3^x), quando x->
, - lim (3^x), quando x-> =
=  -
-
 = lim (1 - 2^x),quando x->
= lim (1 - 2^x),quando x-> / lim (1 - 3^x), quando x->
/ lim (1 - 3^x), quando x->


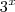 se aproxima de infinito mais rapidamente que
se aproxima de infinito mais rapidamente que 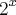 , pois
, pois  . Assim, o primeiro limite vai para
. Assim, o primeiro limite vai para  .
. . A estratégia é tentar reescrevê-lo de tal modo que não haja mais indeterminação. Para isso, note que colocando
. A estratégia é tentar reescrevê-lo de tal modo que não haja mais indeterminação. Para isso, note que colocando 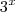 em evidência obtemos:
em evidência obtemos:![\lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty \lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty](/latexrender/pictures/a27ac0e1686c0171f437b9e3073528b0.png)
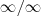 . Para remover esta indeterminação, note que dividindo o numerador e o denominador por
. Para remover esta indeterminação, note que dividindo o numerador e o denominador por