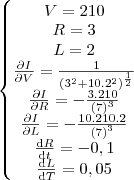"Num determinado circuito elétrico, a corrente 'I' é dada, em função da voltagem 'V', da resistência 'R' e da indutância 'L' por
![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png) . No instante em que 'V' é 210 volts, R é igual a 3 ohms e está decaindo a uma taxa de 0,1 ohms por segundo, enquanto que 'L' é igual a 2 henrys e está crescendo a uma razão de 0,05 henrys por segundo. Qual deve ser a variação de 'V', neste instante, para que a corrente permaneça constante?". Resposta = 3 volts por segundo.
. No instante em que 'V' é 210 volts, R é igual a 3 ohms e está decaindo a uma taxa de 0,1 ohms por segundo, enquanto que 'L' é igual a 2 henrys e está crescendo a uma razão de 0,05 henrys por segundo. Qual deve ser a variação de 'V', neste instante, para que a corrente permaneça constante?". Resposta = 3 volts por segundo.COMO TENTEI RESOLVER: primeiro achei o valor de I através da substituição dos valores fornecidos pelo enunciado na equação
![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png) , ficando desta forma:
, ficando desta forma: ![I = \frac{210}{\sqrt[2]{49}} = 30 I = \frac{210}{\sqrt[2]{49}} = 30](/latexrender/pictures/6fcf1c943af983c604e6cc3e103f0bd9.png) . Após encontrar o valor de I, este foi igualado às derivadas de I em função das variáveis
. Após encontrar o valor de I, este foi igualado às derivadas de I em função das variáveis 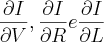 e multipliquei cada derivada parcial por sua respectiva taxa de variação
e multipliquei cada derivada parcial por sua respectiva taxa de variação 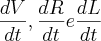 ; lembrando que o valor que quero encontrar é
; lembrando que o valor que quero encontrar é 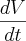 ; assim ficou:
; assim ficou: 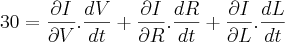 .
. Resolvendo as derivadas, encontrei:
![\frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} \frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/5188559259bcaf6892cdd4568d69f646.png) ;
; ![\frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}} \frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}}](/latexrender/pictures/e597083528a8fa235ef71e3aed37b69f.png) ; e
; e ![\frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}} \frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}}](/latexrender/pictures/336bcda187ceec6ab911e2912aaecf7d.png) .
.Fazendo desta forma encontrei um valor na ordem de 200, ou seja, muito distante da resposta correta (3 volts/s). Refiz diversas vezes e não saiu deste resultado.
Desde já agradeço a ajuda. Forte abraço!
jpreis


 que depende de 3 variáveis
que depende de 3 variáveis 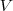 ,
, 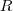 e
e 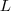 as quais dependem do tempo
as quais dependem do tempo  . Assim, a derivada total de
. Assim, a derivada total de 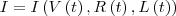
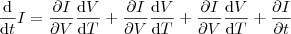 .
.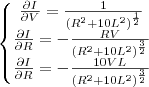
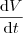 no instante indicado, para que a corrente se mantenha constante, isto é,
no instante indicado, para que a corrente se mantenha constante, isto é, 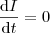 , então basta substituir na relação da derivada e teremos um resultado. Veja que no instante indicado temos
, então basta substituir na relação da derivada e teremos um resultado. Veja que no instante indicado temos