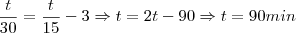por Celma » Seg Jul 15, 2013 22:42
por Celma » Seg Jul 15, 2013 22:42
Boa noite!
Eu não consigo entender como é possível calcular o tempo se, em ambos os casos, o tempo já foi informado.
A partir de um valor inicial igual a 16000, certa população P1 de bactérias dobra a cada 30 minutos. Simultaneamente, partindo de um valor inicial 8 vezes menor, outra população P2 de bactérias cresce, dobrando de valor a cada 15 minutos. Em qual instante t as duas populações terão o mesmo valor?
P1 = P2

Muito obrigada!
-
Celma
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Jun 28, 2013 12:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por Russman » Seg Jul 15, 2013 23:55
por Russman » Seg Jul 15, 2013 23:55
A população
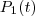
é função do tempo com período
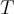
, que no caso é de 30 min. O mesmo acontece para a população
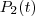
que também é função do tempo com período
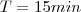
. As equações que regem o crescimento das populações são
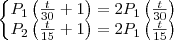
cuja solução é, identificando a equação de progressões geométricas,
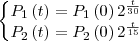
O problema informa que
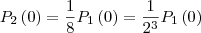
de modo que
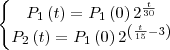
e ainda pede em que instante as populações terão o mesmo valor. Para isto temos de calcular para qual

que

.
Facilmente simplificamos o problema para
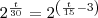
.
Ou seja, quando
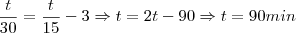
ou seja, após decorridos 90 minutos de crescimento ambas populações terão o mesmo número de indivíduos.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



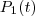 é função do tempo com período
é função do tempo com período 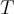 , que no caso é de 30 min. O mesmo acontece para a população
, que no caso é de 30 min. O mesmo acontece para a população 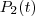 que também é função do tempo com período
que também é função do tempo com período 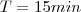 . As equações que regem o crescimento das populações são
. As equações que regem o crescimento das populações são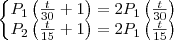
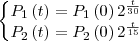
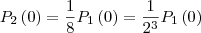 de modo que
de modo que 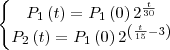
 que
que  .
.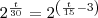 .
.