 por hygorvv » Dom Jun 30, 2013 09:31
por hygorvv » Dom Jun 30, 2013 09:31
Olá galera, bom dia.
Resolvendo alguns exercícios de limites de duas variáveis (sem possuir resposta rs) me deparei com uma divergência entre minha resposta e a do Wolframalpha. Encontrei 0 e o wolfram diz que não existe. Segue a questão e como resolvi.
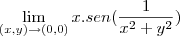
Pensei assim:
Como a função seno é limitada, temos:
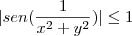
Como
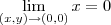
, temos que o limite será zero.
Alguém pode me ajudar?
Agradeço desde já.
Até breve.
-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Man Utd » Ter Jul 29, 2014 19:20
por Man Utd » Ter Jul 29, 2014 19:20
Olá

O wolfram aqui diz primeiro que não existe limite, mas logo depois diz que existe e é igual a zero.
http://www.wolframalpha.com/input/?i=li ... 280%2C0%29 Minha Opinião: Não use o wolfram para calcular limite de função de várias variavéis, ele simplesmente erra vários tipos de limite.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite]Limite de duas variaveis
 por amigao » Seg Nov 25, 2013 18:14
por amigao » Seg Nov 25, 2013 18:14
- 4 Respostas
- 3296 Exibições
- Última mensagem por amigao

Ter Nov 26, 2013 19:36
Cálculo: Limites, Derivadas e Integrais
-
- Limite de duas variaveis
por Tixa11 » Seg Abr 01, 2013 13:13
- 1 Respostas
- 2207 Exibições
- Última mensagem por young_jedi

Qua Abr 03, 2013 11:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Duas variaveis
por fabriel » Sáb Jun 15, 2013 16:48
- 2 Respostas
- 2494 Exibições
- Última mensagem por temujin

Sáb Jun 15, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Limite de Função de Duas Variáveis
por raimundoocjr » Qui Out 10, 2013 22:29
- 0 Respostas
- 1656 Exibições
- Última mensagem por raimundoocjr

Qui Out 10, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limite - Duas Variáveis (Indeterminação)]
por raimundoocjr » Qui Out 17, 2013 21:55
- 1 Respostas
- 3649 Exibições
- Última mensagem por Man Utd

Ter Jun 17, 2014 13:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
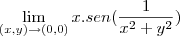
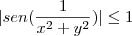
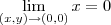 , temos que o limite será zero.
, temos que o limite será zero.




 .
.



