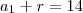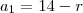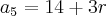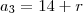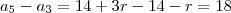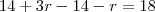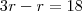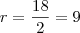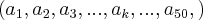
Onde
 e
e 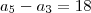 ,
, 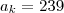 , então k é igual a quanto ?
, então k é igual a quanto ?Na formula para do
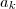 temo isso não é:
temo isso não é: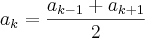
mas como encontrar o k ?
Essa eu não compreendi

só sei isso com esse k :(
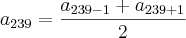

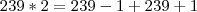
No caso o
 é o último número, o n é a quantidade de termos da P.A, o
é o último número, o n é a quantidade de termos da P.A, o 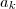 seria a media aritmética entre o antecedente e o consequente...
seria a media aritmética entre o antecedente e o consequente...e o k seria o que ?
Estou totalmente fora do rumo nos pensamentos... alguém pode me dar uma ajuda do caminho? Agradeço desde já por a atenção de quem se der o trabalho de ajudar, muito obrigado mesmo ...