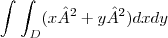, onde D é a região do 1 quadrante limitada pelos hiperbóles:[s]Obs:[/s] Ignore o A² , é apenas x²+y² , ainda não sei mexer nesse latex direito!!
x²-y² = 1
x²-y²=9
xy=2
xy=4
O que eu fiz até agora:
u = x²-y²
v = xy
Novos limites de integração:
Para u, de 1 a 9
Para v, de 2 a 4
Fiz o determinante matriz jacobiana J(u,v) = l Ux Vx l
l Uy Vy l
O determinante da Jacobiana (u,v) deu 2 ( x² + y² ) , logo, dudv = 2(x²+y²)dxdy => dxdy = dudv/(2(x²+y²))
Depois substitui na integral inicial, cortei os x²+y² , e ficou 1/2dxdv com os intervalos de integração que eu falei alí em cima.
Enfim, não esta conseguindo resolver nenhum exercício de integral dupla deste tipo, consegui esse, e fiquei na maior dúvida, isso tá certo ou fiz alguma besteira?
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.