o exercicio pede para mostra que a combinação não é divisivel por 7
(considere esse simbolo como o de combinação) o livro resolve assim:encontro os multiplos de 7 em 1000, assim temos que de 7 ate 994 tenho 142 multiplos/divisores de 7 e analisando melhor encontro de 49 ate 980 tenho 20 multiplos/divisiveis por
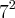e sabendo que existe 2 multiplos/divisiveis por 
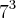assim tenho 142+20+2=164, faço isso com o 500 e de 7 ate 497 tenho 71 multiplos/divisores de 7 e analisando de 49 ate 490 encontro 10 multiplos/divisiveis por 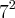e sabendo que existe 1 multiplo/divisivel por 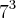assim tenho 71+2+10=82 só que ele multiplica esse 82 por 2 obtenho 164 eu estou pensando que seja devido o 500 estar elevado ao quadrado na formula aqui abaixo
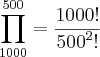(lembrando em considerar esse simbolo como o da combinação), chegando aqui ele conclui que essa combinação não é divisivel por 7.
.
