O Nível de pressão sonora (L) é "dado" em decibel (dB). E a fórmula pra calculá-lo (apartir de p, que é pressão sonora) se dá por:
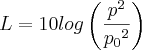, onde 
Por ser logarítmico, não dá pra dizer por exemplo, que 50 dB + 50 dB = 100 dB.
Porém há uma relação para esse tipo de soma. Pode-se dizer que
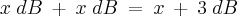
No entanto eu não sei como provar isso. Essa é a questão. Como se faz pra prová-lo?
Se for de ajuda, tenho que
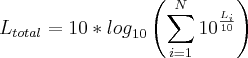, onde 
é a N somas de vários L (no caso talvez poderia ser tratado L+L... sei lá...).[i]PS: Sinto-me na obrigação de dizer que dB NÃO É UNIDADE de nível de pressão sonora. É uma pseudounidade, afinal não se utiliza unidade em 'níveis'.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.