 por fabriel » Seg Jun 03, 2013 16:47
por fabriel » Seg Jun 03, 2013 16:47
Oi pessoal me deparei com esse exerciio:
se A ou B é uma matriz não inversível então A.B também não é, Prove isto sem usar determinantes.Como vou provar isso, sem usar um caso particular, por exemplo eu usei esse produto das duas matrizes respectivamente A e B.
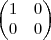
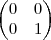
Que realizando o produto resulataria na matriz nulo, e seu determinante seria nulo, portanto não apresentaria tbm inversão.
Mas como vou provar isso sem usar determinantes??
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Seg Jun 03, 2013 18:48
por e8group » Seg Jun 03, 2013 18:48
Pensei da seguinte forma :
Suponha
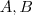
matrizes
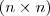
e
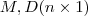
.
Seja

solução do sistema

.Multiplicando-se pela esquerda ambos lados da igualdade por

,aplicando a propriedade associativa e considerando

,temos :
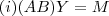
.Agora para mostrar que
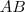
não é invertível basta mostrar que o sistema
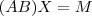
admite outra solução .Para isto ,considere

outra solução do sistema

(note que podemos usar que o sistema

admite outra solução, pois ,por hipótese
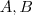
são singulares ) .Assim ,novamente multiplicando-se pela esquerda ambos lados da igualdade por

e por associatividade ,obtemos :
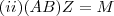
. Agora você pode concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinantes - cálculo matriz nxn (aplicar propriedades)
por emsbp » Qua Out 10, 2012 09:25
- 2 Respostas
- 3694 Exibições
- Última mensagem por emsbp

Qua Out 10, 2012 16:43
Matrizes e Determinantes
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4487 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
-
- Matriz - Inversa ou não?
por Bruhh » Seg Mar 08, 2010 16:31
- 7 Respostas
- 16129 Exibições
- Última mensagem por Neperiano

Qui Mar 11, 2010 15:50
Conversão de Unidades
-
- [Matriz Inversa]
por vanessafey » Seg Set 12, 2011 15:17
- 4 Respostas
- 3283 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 23:23
Matrizes e Determinantes
-
- Matriz Inversa
por Claudin » Qui Set 15, 2011 17:44
- 11 Respostas
- 5283 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 18:51
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
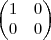
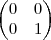


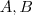 matrizes
matrizes 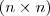 e
e 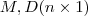 .
. solução do sistema
solução do sistema  .Multiplicando-se pela esquerda ambos lados da igualdade por
.Multiplicando-se pela esquerda ambos lados da igualdade por  ,aplicando a propriedade associativa e considerando
,aplicando a propriedade associativa e considerando  ,temos :
,temos : 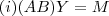 .Agora para mostrar que
.Agora para mostrar que 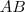 não é invertível basta mostrar que o sistema
não é invertível basta mostrar que o sistema 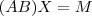 admite outra solução .Para isto ,considere
admite outra solução .Para isto ,considere  outra solução do sistema
outra solução do sistema  (note que podemos usar que o sistema
(note que podemos usar que o sistema  admite outra solução, pois ,por hipótese
admite outra solução, pois ,por hipótese 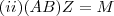 . Agora você pode concluir .
. Agora você pode concluir .





