 por 380625 » Sáb Jun 01, 2013 16:57
por 380625 » Sáb Jun 01, 2013 16:57
Boa tarde preciso mostrar que
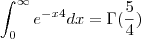
, onde
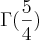
se trata da função Gama.
O que fiz usei a série de Maclaurin do lado esquerdo e desenvolvi alguns termos e encontrei o termo geral.
Depois integrei a série termo a termo porém não consigo achar uma relação com a função gama.
Espero que alguem possa me dar uma ajuda por ai.
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por e8group » Dom Jun 02, 2013 20:04
por e8group » Dom Jun 02, 2013 20:04
Não se está correto ,mas pensei assim :
Aceitando que

,temos :
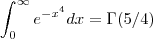
.Pois ,fazendo a substiuição

,obtemos
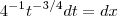
.Assim ,
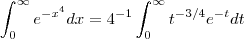
.Utilizando o método de integração por partes ,resulta
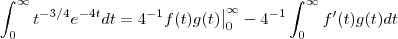
em que :
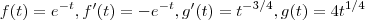
.
Daí ,
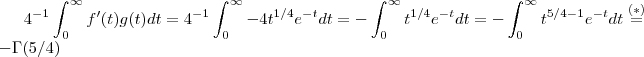
.
Lembrando que
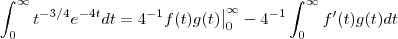
e mostrando que
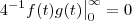
(deixo como exercício p/ vc) segue o resultado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Gama
por grilo » Dom Set 30, 2012 13:20
- 1 Respostas
- 982 Exibições
- Última mensagem por MarceloFantini

Dom Set 30, 2012 13:47
Cálculo: Limites, Derivadas e Integrais
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5576 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4590 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5746 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3487 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
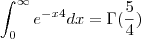 , onde
, onde 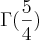 se trata da função Gama.
se trata da função Gama.

 ,temos :
,temos : 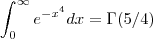 .Pois ,fazendo a substiuição
.Pois ,fazendo a substiuição  ,obtemos
,obtemos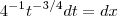 .Assim ,
.Assim , 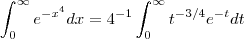 .Utilizando o método de integração por partes ,resulta
.Utilizando o método de integração por partes ,resulta 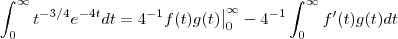 em que :
em que : 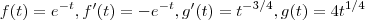 .
. 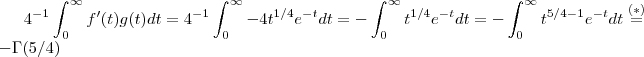 .
. 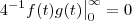 (deixo como exercício p/ vc) segue o resultado .
(deixo como exercício p/ vc) segue o resultado .