 por ferfer » Dom Mai 26, 2013 13:38
por ferfer » Dom Mai 26, 2013 13:38
Mostre que, ?n ? Z, o mdc( 2n+1 , n(n+1)/2) = 1
Então, eu fiz um parecido que era provar o mdc( 2n + 1 , n), usando o algoritmo de Euclides... só que foi fácil!
Este que postei no forum, eu não consegui desenvolver! Há outra maneira sem algoritmo de Euclides?
Obrigado
-
ferfer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 26, 2013 13:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por e8group » Dom Mai 26, 2013 15:48
por e8group » Dom Mai 26, 2013 15:48
Já pensou em supor dois casos : 1°) caso :

é impar ; 2º) caso :

é par ,para ambos casos , existe algum número inteiro
![k[tex] tal que se [tex] n k[tex] tal que se [tex] n](/latexrender/pictures/2006e4268147d11421ceb66b0c35265e.png)
é impar então
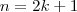
;caso contrário
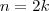
. Tente analisar os dois casos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ferfer » Seg Mai 27, 2013 10:53
por ferfer » Seg Mai 27, 2013 10:53
Santhiago,
Obrigado pela resposta.
Então, numa questão que é necessário provar, eu posso substituir os casos (par e ímpar) por números? Ou vc não queria dizer isso?
Porque os exercícios de 'calcule' eu consigo realizar tranquilamente. Já os de 'prove', tenho esta dificuldade.
Obrigado
-
ferfer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 26, 2013 13:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por e8group » Seg Mai 27, 2013 23:31
por e8group » Seg Mai 27, 2013 23:31
Outra alternativa que pensei .
Podemos escrever que

.Assim , se

, então

divide
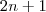
e

.Mas ,desde que

divide

,necessariamente

dividirá

ou

.Analisando ambos casos ,pela igualdade

concluímos que
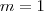
(pois caso contrário ele não dividiria ,
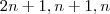
nem mesmo

)
ferfer escreveu:Santhiago,
Obrigado pela resposta.
Então, numa questão que é necessário provar, eu posso substituir os casos (par e ímpar) por números? Ou vc não queria dizer isso?
Porque os exercícios de 'calcule' eu consigo realizar tranquilamente. Já os de 'prove', tenho esta dificuldade.
Obrigado
Não precisamos generalizar .Se

é par então
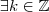
tal que
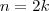
,e se ele for impar
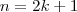
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Mai 30, 2013 13:09
por e8group » Qui Mai 30, 2013 13:09
Obs .: Foi mencionado que

divide

e

,mas isto não foi provado.Esta prova é simples,ela segue dos itens
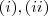
+ hipótese de

.De fato podemos usar
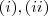
para provar que

divide
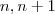
, assim , como
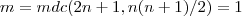
,pois :
![1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1) 1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1)](/latexrender/pictures/d118d4ca271f064e894e8bf387d555a0.png)
que resulta :


Agora,multiplicando

por

e

por

,obtemos
![(*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1 (*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1](/latexrender/pictures/8aae63593f20a9e8b46714a7ac599149.png)
![(**) 4[n(n+1)/2] -n(2n+1) = n (**) 4[n(n+1)/2] -n(2n+1) = n](/latexrender/pictures/be24982750669f68575f27a36aad710e.png)
Suponha que os números inteiros
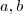
sejam, respectivamente, o resultado da divisão de
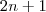
e

por

; assim multiplicando-se
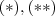
por

(é claro que
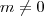
) obtemos ,
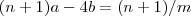
e
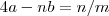
.
Como

então
![[(n+1)a - 4b] \in \mathbb{Z} [(n+1)a - 4b] \in \mathbb{Z}](/latexrender/pictures/87d596f8c1fa0ee620f5ce278d24822c.png)
o que implica

divide

.Analogamente ,chega-se a conclusão que

divide

.
Agora, basta utilizar este resultado + os itens
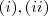
p/ concluir que
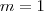
.Espero que ajude .
Por enquanto é isso que pensei em utilizar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ferfer » Qui Mai 30, 2013 13:22
por ferfer » Qui Mai 30, 2013 13:22
Santiago,
Perfeito! Ótima explicação... Deu para entender e evoluir bastante.
Obrigado
-
ferfer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 26, 2013 13:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mostre que:
por Cleyson007 » Seg Jul 11, 2011 22:09
- 1 Respostas
- 1738 Exibições
- Última mensagem por LuizAquino

Ter Jul 12, 2011 09:43
Cálculo: Limites, Derivadas e Integrais
-
- Mostre que:
por Cleyson007 » Sex Abr 27, 2012 12:23
- 1 Respostas
- 1698 Exibições
- Última mensagem por Guill

Sex Abr 27, 2012 21:39
Cálculo: Limites, Derivadas e Integrais
-
- [Mostre] que
por NicoleNicolela » Qua Abr 10, 2013 20:15
- 2 Respostas
- 2489 Exibições
- Última mensagem por e8group

Qua Abr 10, 2013 23:49
Funções
-
- Mostre que a é racional!
por Abelardo » Qui Abr 14, 2011 00:01
- 0 Respostas
- 1209 Exibições
- Última mensagem por Abelardo

Qui Abr 14, 2011 00:01
Álgebra Elementar
-
- [Fatoração] Mostre
por chronoss » Dom Abr 21, 2013 15:44
- 0 Respostas
- 1059 Exibições
- Última mensagem por chronoss

Dom Abr 21, 2013 15:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é impar ; 2º) caso :
é impar ; 2º) caso : ![k[tex] tal que se [tex] n k[tex] tal que se [tex] n](/latexrender/pictures/2006e4268147d11421ceb66b0c35265e.png) é impar então
é impar então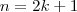 ;caso contrário
;caso contrário 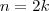 . Tente analisar os dois casos .
. Tente analisar os dois casos .
 .Assim , se
.Assim , se  , então
, então  divide
divide 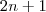 e
e  .Mas ,desde que
.Mas ,desde que  .Analisando ambos casos ,pela igualdade
.Analisando ambos casos ,pela igualdade 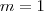 (pois caso contrário ele não dividiria ,
(pois caso contrário ele não dividiria ,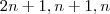 nem mesmo
nem mesmo 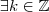 tal que
tal que 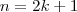 .
.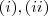 + hipótese de
+ hipótese de 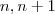 , assim , como
, assim , como 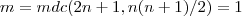 ,pois :
,pois :![1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1) 1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1)](/latexrender/pictures/d118d4ca271f064e894e8bf387d555a0.png) que resulta :
que resulta : 

 por
por  por
por ![(*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1 (*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1](/latexrender/pictures/8aae63593f20a9e8b46714a7ac599149.png)
![(**) 4[n(n+1)/2] -n(2n+1) = n (**) 4[n(n+1)/2] -n(2n+1) = n](/latexrender/pictures/be24982750669f68575f27a36aad710e.png)
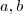 sejam, respectivamente, o resultado da divisão de
sejam, respectivamente, o resultado da divisão de 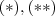 por
por  (é claro que
(é claro que 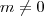 ) obtemos ,
) obtemos , 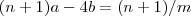
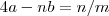 .
.  então
então ![[(n+1)a - 4b] \in \mathbb{Z} [(n+1)a - 4b] \in \mathbb{Z}](/latexrender/pictures/87d596f8c1fa0ee620f5ce278d24822c.png) o que implica
o que implica 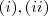 p/ concluir que
p/ concluir que 




