![\int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}} \int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}}](/latexrender/pictures/ab02e1099c21f28714e1f5d385c79205.png)
o resultado deveria ser:1/2ln
![\left|\sqrt[]{4{x}^{2}+9}+2x \right| \left|\sqrt[]{4{x}^{2}+9}+2x \right|](/latexrender/pictures/1d15708126a90c9cdc62789391d39666.png)
Mas o meu resutado não está bantendo: 1/2ln
![\left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right| \left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right|](/latexrender/pictures/944ba177e3545569bbae0a5d83c4563d.png)
Não sei onde estou errando, por favor me ajudem!

![\int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}} \int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}}](/latexrender/pictures/ab02e1099c21f28714e1f5d385c79205.png)
![\left|\sqrt[]{4{x}^{2}+9}+2x \right| \left|\sqrt[]{4{x}^{2}+9}+2x \right|](/latexrender/pictures/1d15708126a90c9cdc62789391d39666.png)
![\left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right| \left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right|](/latexrender/pictures/944ba177e3545569bbae0a5d83c4563d.png)

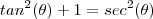 .Escrevendo o radicando
.Escrevendo o radicando 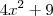 como
como 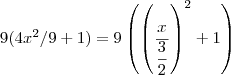 .Lembrando da identidade mencionada acima ,fica fácil ver que a substituição que vamos fazer é :
.Lembrando da identidade mencionada acima ,fica fácil ver que a substituição que vamos fazer é : 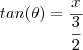 e ainda para que
e ainda para que 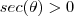 deveremos impor
deveremos impor 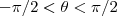 .Como
.Como 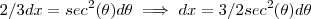 ,temos que :
,temos que : 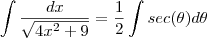 .
. e realizar uma nova substituição ,
e realizar uma nova substituição , 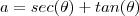 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)