 por Man Utd » Dom Mai 26, 2013 16:02
por Man Utd » Dom Mai 26, 2013 16:02
Calcule a derivada da seguinte função
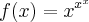
.
comecei assim:

é isso? se não alguém pode me dar dicas?

obrigado desde já.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Dom Mai 26, 2013 16:26
por e8group » Dom Mai 26, 2013 16:26
Considere :
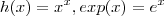
.Temos :

.Assim , pela regra da cadeia ,
![f'(x) = ([h'\circ h] \cdot h')(x) = \frac{d h(h(x))}{d(h(x))} \cdot \frac{dh(x)}{dx} f'(x) = ([h'\circ h] \cdot h')(x) = \frac{d h(h(x))}{d(h(x))} \cdot \frac{dh(x)}{dx}](/latexrender/pictures/5d3900b0056647c5561907e53e2afd7a.png)
. Como
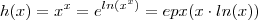
.Novamente pela regra da cadeia ,temos :
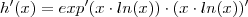
que devido a regra do produto ,

.
(Claro que está implícito
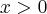
) .
Lembrando que :
![f'(x) = ([h'\circ h] \cdot h')(x) = h'(h(x)) \cdot h'(x) f'(x) = ([h'\circ h] \cdot h')(x) = h'(h(x)) \cdot h'(x)](/latexrender/pictures/4851758e48d8839d2a9b9d5515606f86.png)
.Basta substituir o resultado acima .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Dom Mai 26, 2013 17:50
por Man Utd » Dom Mai 26, 2013 17:50
olá santhiago,eu não posso deixar do jeito que está?(Verifiquei a resposta no wolfram:
http://www.wolframalpha.com/input/?i=de ... x%5Ex%29+# )
obrigado pela paciência.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Dom Mai 26, 2013 19:00
por e8group » Dom Mai 26, 2013 19:00
Pode sim ,uma vez que elas são equivalentes .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integração e Diferenciação são de fato FUNÇÕES?
por Jhenrique » Qui Set 13, 2012 02:30
- 1 Respostas
- 1146 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:12
Funções
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2329 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1783 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1387 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1601 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
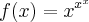 .
.


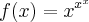 .
.


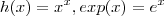 .Temos :
.Temos :  .Assim , pela regra da cadeia ,
.Assim , pela regra da cadeia , ![f'(x) = ([h'\circ h] \cdot h')(x) = \frac{d h(h(x))}{d(h(x))} \cdot \frac{dh(x)}{dx} f'(x) = ([h'\circ h] \cdot h')(x) = \frac{d h(h(x))}{d(h(x))} \cdot \frac{dh(x)}{dx}](/latexrender/pictures/5d3900b0056647c5561907e53e2afd7a.png) . Como
. Como 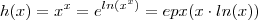 .Novamente pela regra da cadeia ,temos :
.Novamente pela regra da cadeia ,temos : 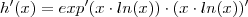 que devido a regra do produto ,
que devido a regra do produto ,  .
.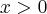 ) .
) .![f'(x) = ([h'\circ h] \cdot h')(x) = h'(h(x)) \cdot h'(x) f'(x) = ([h'\circ h] \cdot h')(x) = h'(h(x)) \cdot h'(x)](/latexrender/pictures/4851758e48d8839d2a9b9d5515606f86.png) .Basta substituir o resultado acima .
.Basta substituir o resultado acima .

