 por Pedro123 » Qui Mai 23, 2013 16:41
por Pedro123 » Qui Mai 23, 2013 16:41
Olá galera, estou com dúvida na seguinte questão, fiz a materia ja tem mais de 2 anos e nao lembro bem como resolver, consegui fazer o óbvio que é igualar o produto escalar dos vetores normais dos planos a zero, porém nao fui muito além disso. Aqui está a questão:
Determinar os valores de a e b de modo que os planos
PI1: ax+by+4z -1 =0
PI2: 3x-5y-2z+5 =0
sejam perperdiculares
Me parece ser algo bem simples, porém nao estou enxergando.
Grato pela atenção
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por e8group » Dom Mai 26, 2013 14:04
por e8group » Dom Mai 26, 2013 14:04
Sim está certo , como
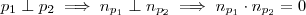
.Onde :
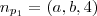
e
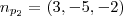
são ,respectivamente ,vetores ortogonais aos planos
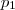
e
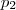
. Através da equação
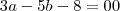
,obtemos
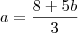
isto nos faz pensar que

é um número arbitrário . Mas ,tomando-se arbitrariamente dois pontos que pertencem ao plano
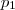
, poderemos construir um vetor ortogonal a
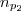
.Por exemplo , fazendo-se
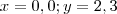
na equação no plano
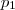
e obtemos que os pontos
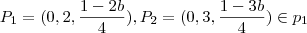
. Assim ,
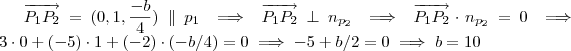
.
Logo ,lembrando que
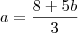
,temos que
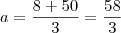
.
Verificando a resposta : 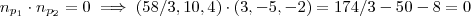
. (OK!!)
Se não falhei em algum conceito é isso .
Justificativa em relação a escolha arbitrária dos pontos

. Suponha que
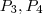
são pontos genéricos do plano
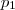
. Assim ,
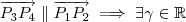
tal que
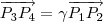
.
Daí ,
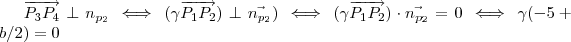
.
Como as equações são equivalentes é fácil verificar a unicidade da resposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pedro123 » Seg Mai 27, 2013 14:36
por Pedro123 » Seg Mai 27, 2013 14:36
Muito obrigado santhiago, até pensei em fazer um outro vetor, mas achei que haveria um jeito menos arbitrário de encontrar o mesmo e acabei me confundindo. Enfim, obrigado.
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8159 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10532 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11565 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13607 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9146 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


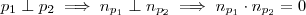 .Onde :
.Onde : 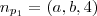 e
e 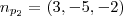 são ,respectivamente ,vetores ortogonais aos planos
são ,respectivamente ,vetores ortogonais aos planos 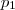 e
e 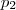 . Através da equação
. Através da equação 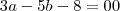 ,obtemos
,obtemos 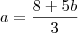 isto nos faz pensar que
isto nos faz pensar que  é um número arbitrário . Mas ,tomando-se arbitrariamente dois pontos que pertencem ao plano
é um número arbitrário . Mas ,tomando-se arbitrariamente dois pontos que pertencem ao plano 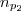 .Por exemplo , fazendo-se
.Por exemplo , fazendo-se 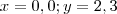 na equação no plano
na equação no plano 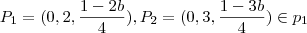 . Assim ,
. Assim , 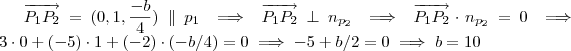 .
. 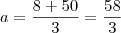 .
.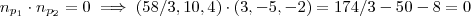 . (OK!!)
. (OK!!) . Suponha que
. Suponha que 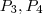 são pontos genéricos do plano
são pontos genéricos do plano 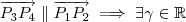 tal que
tal que 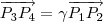 .
. 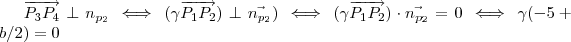 .
. 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  por
por  .
.
