 por Jhennyfer » Dom Mai 19, 2013 13:43
por Jhennyfer » Dom Mai 19, 2013 13:43
Oi, eu sei q é super fácil mas eu não to conformada com esse calculo, tem algo errado.
![\frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}} \frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}}](/latexrender/pictures/69a29da537b1ad6c66b7a364936a962f.png)
Na minha resolução... eu comecei racionalizando as fatores da soma, e ficou assim:
![\frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4} \frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4}](/latexrender/pictures/48e6cf763e1375191e9c6095e00f21ec.png)
e tirando o mmc...
![\frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4} \frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4}](/latexrender/pictures/e679108555abe928556b11011bc38917.png)
----
![\frac{-4-\sqrt[]{15}}{-4} \frac{-4-\sqrt[]{15}}{-4}](/latexrender/pictures/d7ce4220c475c45329804e8abd0458c8.png)
E no gabarito está
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 19, 2013 15:27
por e8group » Dom Mai 19, 2013 15:27
Note que
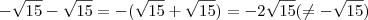
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Mai 19, 2013 15:38
por Jhennyfer » Dom Mai 19, 2013 15:38
isso fica no numerador após tirar o mmc? e o -2-2? fica como? -4-2(raiz² de 15)
Não entendi =/
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 19, 2013 15:46
por e8group » Dom Mai 19, 2013 15:46
Jhennyfer escreveu:isso fica no numerador após tirar o mmc? e o -2-2? fica como? -4-2(raiz² de 15)
Não entendi =/
Sim .O numerador fica :
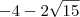
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Mai 19, 2013 15:54
por Jhennyfer » Dom Mai 19, 2013 15:54
Mas então porque no gabarito fica
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
?????
![\frac{-4-2 \sqrt[]{15}}{-4} \frac{-4-2 \sqrt[]{15}}{-4}](/latexrender/pictures/5949a3b4548c95dc4143715439e2b24f.png)
e agora? que propriedades eu uso para esses 4 ficarem 2 e o dois que multiplica a raiz sumir?
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 19, 2013 15:58
por e8group » Dom Mai 19, 2013 15:58
E se você deixar o número dois em evidência ,o que acontece ?
Exemplo :
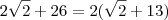
(Distributiva)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Mai 19, 2013 16:09
por Jhennyfer » Dom Mai 19, 2013 16:09
![\frac{2(-2-\sqrt[]{15})}{-4} \frac{2(-2-\sqrt[]{15})}{-4}](/latexrender/pictures/29ecaf1a9719881ecd5ec9131f450418.png)
em cima deu certo agora eu divido esse 2 e 4?
assim:
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 19, 2013 16:14
por e8group » Dom Mai 19, 2013 16:14
Isto mesmo ,estar correto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Mai 19, 2013 16:19
por Jhennyfer » Dom Mai 19, 2013 16:19
Só achei que ficou confuso na questão dos sinais, pois 2 é positivo e 4 é negativo,
com isso pensei que o denominador teria que ser negativo.
Santhiago, conhece algum vídeo aula breve e que possa me ajudar mais com esses calculos numéricos?
pois eles me perseguem, sempre me confundo em alguma coisa. ou algum material da internet.
Já pesquisei, mas só vem coisas q não tem haver com o assunto q eu quero.
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 19, 2013 16:38
por e8group » Dom Mai 19, 2013 16:38
Jhennyfer escreveu:Só achei que ficou confuso na questão dos sinais, pois 2 é positivo e 4 é negativo,
com isso pensei que o denominador teria que ser negativo.
Santhiago, conhece algum vídeo aula breve e que possa me ajudar mais com esses calculos numéricos?
pois eles me perseguem, sempre me confundo em alguma coisa. ou algum material da internet.
Já pesquisei, mas só vem coisas q não tem haver com o assunto q eu quero.
Conheço 3 canais no youtube que dispõe videos aulas sobre este assunto ,são eles :
i)
http://www.youtube.com/user/nerckie/ ou através do site
http://www.vestibulandia.com.br/ ( OBS :Veja a seção Matemática Zero)
ii)
http://www.youtube.com/user/gusalberto8 ... rid&view=1iii)
http://www.youtube.com/user/matematicarioHá outras opções também ,mas no momento não estou lembrando .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Mai 19, 2013 16:45
por Jhennyfer » Dom Mai 19, 2013 16:45
ok, eu já os conhecia, porém eles abordam esses assuntos separadamente, o meu problema é tudo junto...
o jeito vai ser olhar tudo do zero mesmo e tirar as dúvidas. Obrigado a ajuda

-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo Numérico]Problema de Cálculo Numérico
por Piva » Qua Abr 11, 2012 15:10
- 1 Respostas
- 2969 Exibições
- Última mensagem por LuizAquino

Qui Abr 12, 2012 11:58
Cálculo: Limites, Derivadas e Integrais
-
- calculo numerico
por ehrefundini » Qua Mai 07, 2008 10:31
- 1 Respostas
- 2100 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 11:02
Pedidos de Materiais
-
- Calculo Numerico !!
por laisgomes2107 » Sex Set 19, 2008 01:06
- 2 Respostas
- 2948 Exibições
- Última mensagem por admin

Ter Set 23, 2008 18:35
Dúvidas Pendentes (aguardando novos colaboradores)
-
- calculo numerico
por ehrefundini » Sex Mar 06, 2009 10:36
- 1 Respostas
- 2687 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 13:10
Cálculo Numérico e Aplicações
-
- CALCULO NUMÉRICO I
por futuro fisico » Ter Set 27, 2011 21:04
- 1 Respostas
- 1744 Exibições
- Última mensagem por LuizAquino

Ter Set 27, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}} \frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}}](/latexrender/pictures/69a29da537b1ad6c66b7a364936a962f.png)
![\frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4} \frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4}](/latexrender/pictures/48e6cf763e1375191e9c6095e00f21ec.png)
![\frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4} \frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4}](/latexrender/pictures/e679108555abe928556b11011bc38917.png)
![\frac{-4-\sqrt[]{15}}{-4} \frac{-4-\sqrt[]{15}}{-4}](/latexrender/pictures/d7ce4220c475c45329804e8abd0458c8.png)
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)

![\frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}} \frac{2+\sqrt[]{3}}{1-\sqrt[]{5}}+\frac{2-\sqrt[]{3}}{1+\sqrt[]{5}}](/latexrender/pictures/69a29da537b1ad6c66b7a364936a962f.png)
![\frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4} \frac{2+\sqrt[]{15}}{-4}+\frac{2+\sqrt[]{15}}{-4}](/latexrender/pictures/48e6cf763e1375191e9c6095e00f21ec.png)
![\frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4} \frac{-2-\sqrt[]{15}-2-\sqrt[]{15}}{-4}](/latexrender/pictures/e679108555abe928556b11011bc38917.png)
![\frac{-4-\sqrt[]{15}}{-4} \frac{-4-\sqrt[]{15}}{-4}](/latexrender/pictures/d7ce4220c475c45329804e8abd0458c8.png)
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)

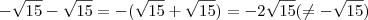 .
.

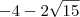 .
.
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
![\frac{-4-2 \sqrt[]{15}}{-4} \frac{-4-2 \sqrt[]{15}}{-4}](/latexrender/pictures/5949a3b4548c95dc4143715439e2b24f.png)

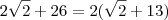 (Distributiva)
(Distributiva)
![\frac{2(-2-\sqrt[]{15})}{-4} \frac{2(-2-\sqrt[]{15})}{-4}](/latexrender/pictures/29ecaf1a9719881ecd5ec9131f450418.png)
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.