 por DanielFerreira » Ter Set 22, 2009 14:10
por DanielFerreira » Ter Set 22, 2009 14:10
No polinômio P(x) = x³ + mx² + m²x - 5, para que P(-1)=2. P(1) é preciso ter:
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Daniel Gurgel » Sáb Out 31, 2009 14:23
por Daniel Gurgel » Sáb Out 31, 2009 14:23
Podemos fazer assim:
*Substituindo (x) por (-1) e igualando a 2. Fazendo as devidas simplificações temos a seguinte equação do segundo grau:

*
Resolvendo a equação no conjunto dos números complexos encontramos:
![m'=\frac{1-i\sqrt[2]{31}}{2} m'=\frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/aec8cc3dbaf056973a3220791c646e25.png)
e
![m"=\frac{1+i\sqrt[2]{31}}{2} m"=\frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/1174083d09889b57972b4b75b312ad7a.png)
*Agora vamos substituir no polinômio, (x) por (1) e m pelos seus respectivos valores ou seja por m' e m".
*Para m'=
![\frac{1-i\sqrt[2]{31}}{2} \frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/2e228b7064ec3e38b57497d953650765.png)
, temos que
![P(1)=-44-4i\sqrt[2]{31} P(1)=-44-4i\sqrt[2]{31}](/latexrender/pictures/93f5c519cf3cd15e06d12f3a37c7ad4b.png)
*Para m"=
![\frac{1+i\sqrt[2]{31}}{2} \frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/e071f34c73b908024dd881421ce8ae68.png)
, temos que
![P(1)=-44+4i\sqrt[2]{31} P(1)=-44+4i\sqrt[2]{31}](/latexrender/pictures/0af6eb5499176266404561d3f3ec0436.png)
-
Daniel Gurgel
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Ago 22, 2009 18:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: concursos
- Andamento: cursando
 por Cleyson007 » Sáb Out 31, 2009 16:20
por Cleyson007 » Sáb Out 31, 2009 16:20
Olá, boa tarde!
Daniel Gurgel, estou resolvendo e não estou encontrando o mesmo resultado. Veja só:
O problema impõe a seguinte condição:

Logo,

Resolvendo, encontra-se a seguinte equação do 2º grau:
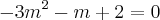
Os valores são:


Se você substituir o valor de

no polinômio

, encontrará a seguinte equação do 3º grau:

.
Calculando o valor de -1 em

, é válida a igualdade.
Logo é preciso ter

.
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Daniel Gurgel » Qui Nov 05, 2009 12:57
por Daniel Gurgel » Qui Nov 05, 2009 12:57
Olá!
Desculpe-me pelo encomodo.
Penssei que a condição do problema era

Até mais.
-
Daniel Gurgel
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Ago 22, 2009 18:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: concursos
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8378 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
-
- Polinômios
por Rose » Seg Set 08, 2008 22:07
- 2 Respostas
- 4655 Exibições
- Última mensagem por Rose

Qua Set 10, 2008 11:50
Polinômios
-
- Polinômios - 3
por DanielFerreira » Ter Set 22, 2009 13:59
- 3 Respostas
- 3089 Exibições
- Última mensagem por DanielFerreira

Qui Fev 10, 2011 09:26
Polinômios
-
- Polinômios - 2
por DanielFerreira » Ter Set 22, 2009 14:00
- 1 Respostas
- 3251 Exibições
- Última mensagem por thadeu

Seg Nov 02, 2009 11:47
Polinômios
-
- Polinômios
por DanielFerreira » Ter Set 22, 2009 14:01
- 2 Respostas
- 2455 Exibições
- Última mensagem por DanielFerreira

Qui Nov 19, 2009 17:59
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![m'=\frac{1-i\sqrt[2]{31}}{2} m'=\frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/aec8cc3dbaf056973a3220791c646e25.png) e
e ![m"=\frac{1+i\sqrt[2]{31}}{2} m"=\frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/1174083d09889b57972b4b75b312ad7a.png)
![\frac{1-i\sqrt[2]{31}}{2} \frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/2e228b7064ec3e38b57497d953650765.png) , temos que
, temos que ![P(1)=-44-4i\sqrt[2]{31} P(1)=-44-4i\sqrt[2]{31}](/latexrender/pictures/93f5c519cf3cd15e06d12f3a37c7ad4b.png)
![\frac{1+i\sqrt[2]{31}}{2} \frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/e071f34c73b908024dd881421ce8ae68.png) , temos que
, temos que ![P(1)=-44+4i\sqrt[2]{31} P(1)=-44+4i\sqrt[2]{31}](/latexrender/pictures/0af6eb5499176266404561d3f3ec0436.png)



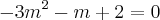


 no polinômio
no polinômio  , encontrará a seguinte equação do 3º grau:
, encontrará a seguinte equação do 3º grau:  .
. , é válida a igualdade.
, é válida a igualdade. .
.

