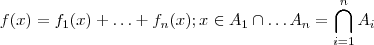por Man Utd » Sex Mai 10, 2013 10:45
por Man Utd » Sex Mai 10, 2013 10:45
Calcule:
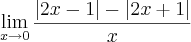
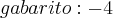
eu não entendi a questão,já resolvi vários limites, mas com somente um módulo,alguém pode me dar uma dica?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sex Mai 10, 2013 11:36
por e8group » Sex Mai 10, 2013 11:36
Bom dia .Basta utilizar a definição de módulo ,conhece ela ? Se não ,suponhamos que temos o seguinte módulo :
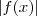
,onde

é uma função elementar .Por definição de módulo , segue-se que
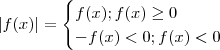
.
No exercício postado tente analisar o sinal de

e
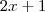
para

em uma vizinhança do número zero .Se nesta vizinhança ,tem-se
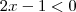
,segue da definição que
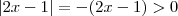
.De forma análoga podemos estudar o outro módulo .Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Sex Mai 10, 2013 12:00
por Man Utd » Sex Mai 10, 2013 12:00
olá eu não entendi bem qual usar:
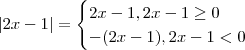
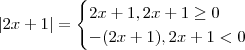
eu ñ sei qual usar,ñ teria q fazer o limite pela direita e pela esquerda?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sex Mai 10, 2013 12:27
por e8group » Sex Mai 10, 2013 12:27
Basta observar se o número

é negativo ou positivo para

em
![(-r,r) [tex] com [tex] r > 0 (-r,r) [tex] com [tex] r > 0](/latexrender/pictures/c96defbfb5ad523420d6a6ede8f259ae.png)
suficiente pequeno . Da mesma forma façamos a mesma análise para
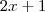
.
Claramente
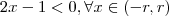
e
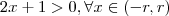
.
Assim ,neste contexto :
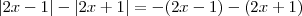
.
Estou sem tempo agora .A noite posso postar mais dicas se necessário ..
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Sex Mai 10, 2013 23:46
por Man Utd » Sex Mai 10, 2013 23:46
santhiago obrigado pela paciência,mas eu não compreendo o porquê desse procedimento,já calculei limites com um só módulo,mas é diferente.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sáb Mai 11, 2013 01:40
por e8group » Sáb Mai 11, 2013 01:40
Vamos tentar novamente . Tome
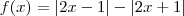
.
Observe que por definição de módulo :
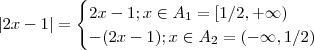
e
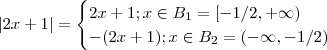
Considere os 4 casos :
1)
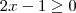 e
e 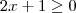
2)
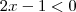 e
e 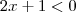
3)
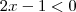 e
e 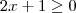
4)
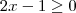 e
e 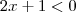
No primeiro caso , tem-se necessariamente
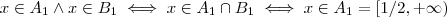
,no segundo ,
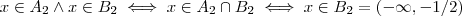
; terceiro ,segue
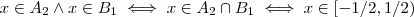
e no último caso , a interseção é vazia .
Assim ,
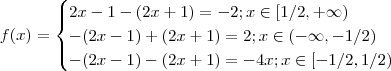
.
Tudo isto é desnecessário para calcular o limite,entretanto como vc estar com dificuldades com soma de módulos(se é assim que podemos dizer ) .Caso teríamos,
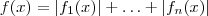
.Por definição de módulo , por exemplo se
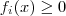
para todo

.Poderíamos definir ,
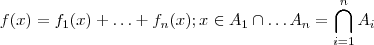
Dica : Estude mais sobre módulos e operações com funções se for necessário .
Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Sáb Mai 11, 2013 14:29
por Man Utd » Sáb Mai 11, 2013 14:29
Muito obrigado pela paciência Santhiago,agora finalmente conseguir entender.

vou dar uma revisada em módulo.Bom final de semana.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite (envolvendo Módulo)
por killerkill » Ter Ago 09, 2011 23:12
- 7 Respostas
- 11130 Exibições
- Última mensagem por LuizAquino

Qua Ago 10, 2011 11:47
Cálculo: Limites, Derivadas e Integrais
-
- limite envolvendo modulo
por matmatco » Qui Mar 22, 2012 23:18
- 7 Respostas
- 4631 Exibições
- Última mensagem por LuizAquino

Ter Mar 27, 2012 13:14
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Modulo em denominador
por orainha » Sex Fev 03, 2017 23:12
- 2 Respostas
- 8305 Exibições
- Última mensagem por orainha

Qui Mar 30, 2017 21:42
Cálculo: Limites, Derivadas e Integrais
-
- [ LIMITE] Limite com módulo!
por mih123 » Qua Set 12, 2012 17:26
- 3 Respostas
- 2575 Exibições
- Última mensagem por LuizAquino

Dom Set 16, 2012 11:11
Cálculo: Limites, Derivadas e Integrais
-
- Módulo
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
- 4 Respostas
- 3031 Exibições
- Última mensagem por MarceloFantini

Sex Mar 05, 2010 16:09
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
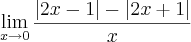
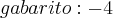

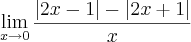
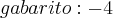

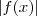 ,onde
,onde  é uma função elementar .Por definição de módulo , segue-se que
é uma função elementar .Por definição de módulo , segue-se que 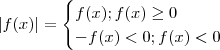 .
.  e
e 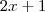 para
para  em uma vizinhança do número zero .Se nesta vizinhança ,tem-se
em uma vizinhança do número zero .Se nesta vizinhança ,tem-se 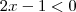 ,segue da definição que
,segue da definição que 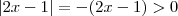 .De forma análoga podemos estudar o outro módulo .Tente concluir .
.De forma análoga podemos estudar o outro módulo .Tente concluir .
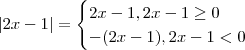
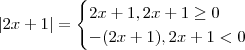

 é negativo ou positivo para
é negativo ou positivo para  em
em ![(-r,r) [tex] com [tex] r > 0 (-r,r) [tex] com [tex] r > 0](/latexrender/pictures/c96defbfb5ad523420d6a6ede8f259ae.png) suficiente pequeno . Da mesma forma façamos a mesma análise para
suficiente pequeno . Da mesma forma façamos a mesma análise para 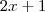 .
. 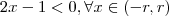 e
e 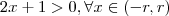 .
. 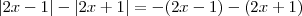 .
. 

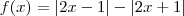 .
.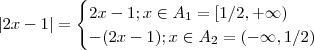
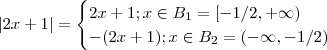
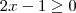 e
e 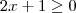
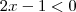 e
e 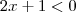
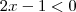 e
e 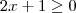
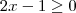 e
e 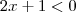
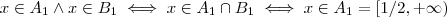 ,no segundo ,
,no segundo , 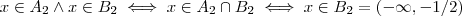 ; terceiro ,segue
; terceiro ,segue 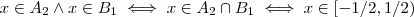 e no último caso , a interseção é vazia .
e no último caso , a interseção é vazia .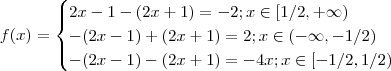 .
.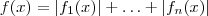 .Por definição de módulo , por exemplo se
.Por definição de módulo , por exemplo se 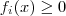 para todo
para todo  .Poderíamos definir ,
.Poderíamos definir ,