 por Sobreira » Dom Mai 05, 2013 16:41
por Sobreira » Dom Mai 05, 2013 16:41
Amigos,
Sei que o fórum é de matematica, mas sabendo que os colaboradores são conhecedores da área de exatas tenho uma dúvida em física.
A lei de Coulomb diz que a força de atração ou repulsão entre duas partículas CARREGADAS é:
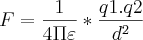
Pois então, a lei de Coulomb fala sobre a interação entre dois corpos carregados ( que possuem número de cargas positivas e negativas diferentes Qtotal=Qpositivo - Qnegativo), portanto quando temos um corpo neutro, o "q"na lei de Coulomb será 0 e portanto a força será 0.
Mas agora a dúvida:
Sabemos muito bem que no processo de eletrização por indução, um corpo carregado é aproximado de uma corpo neutro e quando a distância entre eles é menor do que o raio destes corpos há uma perturbação na distribuição das cargas do corpo neutro e há uma força de atração entre os corpos.Entretanto o corpo neutro não deixou de ser neutro apenas com a aproximação dos corpos (deixaria apenas se colocassemos em contato os corpos).
Como explicar então através da lei de Coulomb a força de interação entre estes corpos sendo que um deles tem "q" igual a 0?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Dom Mai 05, 2013 19:36
por young_jedi » Dom Mai 05, 2013 19:36
temos que o corpo neutro possui cargas positivas e negativas portanto quando um corpo carregado esta a mesma distancia destas cargas positivas e negativas as forças resultantes se anulam, mais se uma das cargas deste corpo neutro estiver mais próximo do corpo carregado então a força desta carga sera maior que a força da outra carga portanto a força resultante não sera 0 então teremos a ação de uma força sobre o corpo. comente qualquer duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Dom Mai 05, 2013 19:56
por Russman » Dom Mai 05, 2013 19:56
interessante a sua pergunta. O amigo ali em cima explicou direitinho o que está por trás desse resultado. Lembre-se que a força é um vetor. Assim, quando um corpo está neutro significa que a força elétrica devido as suas cargas positivas é anulada pela força elétrica devido a suas cargas negativas de forma que em todos os pontos ao seu redor a força resultante é nula. Note que este fato é puramente geomético, isto é, este efeito é devido a distribuição das cargas elétricas. Dessa forma, a eletrização por indução modifica a geometria do problema e a força resultante deixa de ser nula.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Sobreira » Dom Mai 05, 2013 20:49
por Sobreira » Dom Mai 05, 2013 20:49
De um ponto de vista conceitual entendi a questão.
Agora em um exercício, por exemplo, que me desse um corpo carregado com +3q e um corpo neutro (a partir da condição de aproximação haveria uma perturbação na distribuição de cargas, apesar do corpo continuar sendo neutro), logo com q=0. Em termos matemáticos (Lei de Coulomb) como poderia calcular esta força de atração sendo q=0 ??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Russman » Dom Mai 05, 2013 20:57
por Russman » Dom Mai 05, 2013 20:57
No momento que o corpo neutro interage com o carregado por meio da indução ele vai apresentar uma carga induzida. Essa Lei de Coulomb é boa para entender a interação de partículas carregadas. Quando voce agrega muitas delas a situação vai ficando um pouco mais complicada. Por exemplo, se voce aproxima um punhado de partículas carregadas de uma placa condutora ele continuará neutra mas apresentará uma carga superficial induzida devido a presença das cargas proximas. Afinal, a matéria é constituída de partículas carregadas.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida que envolve física.
por Mi_chelle » Seg Abr 25, 2011 15:21
- 2 Respostas
- 2866 Exibições
- Última mensagem por Mi_chelle

Qui Abr 28, 2011 01:47
Geometria Plana
-
- Dúvida Física - Dipolo elétrico.
 por Sobreira » Ter Mai 21, 2013 02:01
por Sobreira » Ter Mai 21, 2013 02:01
- 0 Respostas
- 700 Exibições
- Última mensagem por Sobreira

Ter Mai 21, 2013 02:01
Aritmética
-
- Física
por Mi_chelle » Qua Abr 13, 2011 17:52
- 3 Respostas
- 5036 Exibições
- Última mensagem por Mi_chelle

Qui Abr 14, 2011 00:07
Números Complexos
-
- física
 por leticiapires52 » Sáb Mar 28, 2015 20:10
por leticiapires52 » Sáb Mar 28, 2015 20:10
- 0 Respostas
- 1200 Exibições
- Última mensagem por leticiapires52

Sáb Mar 28, 2015 20:10
Estatística
-
- Questão de Física
por Kelvin Brayan » Dom Mar 06, 2011 19:51
- 2 Respostas
- 9324 Exibições
- Última mensagem por Igor Mirandola

Sex Out 28, 2011 22:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
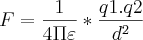


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
