 por samysoares » Sáb Mai 04, 2013 23:06
por samysoares » Sáb Mai 04, 2013 23:06

Por favor, me ajudem. Já tentei o método da substituição e não deu certo!
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sáb Mai 04, 2013 23:36
por e8group » Sáb Mai 04, 2013 23:36
Note que ,
![\frac{t^2-2t}{t^2 +4} = \frac{t^2-2t + [4+(-4)]}{t^2 +4} = \frac{t^2+4-2t-4}{t^2 +4} = \frac{t^2+4}{t^2 +4} - \frac{2t}{t^2 +4} -\frac{4}{t^2 +4} = 1 - \frac{2t}{t^2 +4} - \frac{1}{\left( \dfrac{t}{2}\right )^2 + 1} \frac{t^2-2t}{t^2 +4} = \frac{t^2-2t + [4+(-4)]}{t^2 +4} = \frac{t^2+4-2t-4}{t^2 +4} = \frac{t^2+4}{t^2 +4} - \frac{2t}{t^2 +4} -\frac{4}{t^2 +4} = 1 - \frac{2t}{t^2 +4} - \frac{1}{\left( \dfrac{t}{2}\right )^2 + 1}](/latexrender/pictures/51d185a0193f294a1b0e2818ddd81e55.png)
.
Agora o integrando é mais simples .Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por samysoares » Dom Mai 05, 2013 12:31
por samysoares » Dom Mai 05, 2013 12:31
Obrigada, eu consegui!
Mas se eu fizesse divisão de polinômios daria o mesmo resultado? já qe o grau do numerado é o mesmo do denominador.
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mai 05, 2013 13:34
por e8group » Dom Mai 05, 2013 13:34
samysoares escreveu:Obrigada, eu consegui!
Mas se eu fizesse divisão de polinômios ...
De nada .Neste caso ,após a primeira etapa de divisão de polinômios obteríamos que o grau do resto (que é um polinômio ) seria estritamente menor que o do divisor (que é um polinômio) .Experimente fazer esta divisão .
samysoares escreveu:... daria o mesmo resultado? já qe o grau do numerado é o mesmo do denominador.
Apesar de eles possuírem o mesmo grau , tal resultado não seria equivalente .Sempre após a divisão de um polinômio
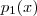
por
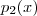
em que

obtemos algo do gênero
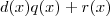
como resposta . Onde :
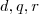
são polinômios .
Se você observar ,após aquele "artifício algébrico " que foi utilizado no integrando, a resposta é da forma
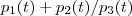
, em que
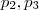
são polinômios tais que

e
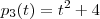
, e claro
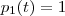
uma função constante . Como podemos ver a resposta não é da forma
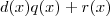
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4591 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4350 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2853 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2881 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\frac{t^2-2t}{t^2 +4} = \frac{t^2-2t + [4+(-4)]}{t^2 +4} = \frac{t^2+4-2t-4}{t^2 +4} = \frac{t^2+4}{t^2 +4} - \frac{2t}{t^2 +4} -\frac{4}{t^2 +4} = 1 - \frac{2t}{t^2 +4} - \frac{1}{\left( \dfrac{t}{2}\right )^2 + 1} \frac{t^2-2t}{t^2 +4} = \frac{t^2-2t + [4+(-4)]}{t^2 +4} = \frac{t^2+4-2t-4}{t^2 +4} = \frac{t^2+4}{t^2 +4} - \frac{2t}{t^2 +4} -\frac{4}{t^2 +4} = 1 - \frac{2t}{t^2 +4} - \frac{1}{\left( \dfrac{t}{2}\right )^2 + 1}](/latexrender/pictures/51d185a0193f294a1b0e2818ddd81e55.png) .
.

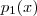 por
por 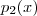 em que
em que  obtemos algo do gênero
obtemos algo do gênero 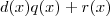 como resposta . Onde :
como resposta . Onde : 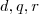 são polinômios .
são polinômios .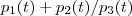 , em que
, em que 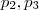 são polinômios tais que
são polinômios tais que  e
e 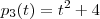 , e claro
, e claro 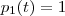 uma função constante . Como podemos ver a resposta não é da forma
uma função constante . Como podemos ver a resposta não é da forma 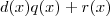 .
.





