 por arthurvct » Sex Mai 03, 2013 20:16
por arthurvct » Sex Mai 03, 2013 20:16
Calcule os coeficientes angulares das retas tangentes às curvas f(x)=
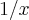
e g(x)=

, no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?
-
arthurvct
-
 por arthurvct » Sex Mai 03, 2013 20:17
por arthurvct » Sex Mai 03, 2013 20:17
alguém pode me dar uma luz?
-
arthurvct
-
 por arthurvct » Sáb Mai 04, 2013 10:45
por arthurvct » Sáb Mai 04, 2013 10:45
ninguém??
-
arthurvct
-
 por marinalcd » Sáb Mai 04, 2013 16:11
por marinalcd » Sáb Mai 04, 2013 16:11
arthurvct escreveu:Calcule os coeficientes angulares das retas tangentes às curvas f(x)=
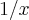
e g(x)=

, no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?
1ª: as derivadas das curvas determinam os coeficientes angulares das retas tangentes, então é só derivar e depois calcular no ponto da interseção (substituir);
2ª: Para descobrir o ângulo, basta você calcular o arcotangente do coeficiente que você encontrar.
As curvas são bem simples e as derivadas também. Tente fazer!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por arthurvct » Qui Mai 16, 2013 19:23
por arthurvct » Qui Mai 16, 2013 19:23
Obrigado! Mas tenho outra dúvida, eu igualei f(x) a g(x) por se tratar do ponto de interseção, achei que x=1, dai eu achei f'(1) e g'(1), deu -1 e 2, mas e agora? como calcular a arcotangente disso? me explica a partir daqui, por favor!! Abraço
-
arthurvct
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Envolvendo Limites e Derivadas Nível Hard
por landerson » Sex Abr 24, 2015 10:32
- 0 Respostas
- 1354 Exibições
- Última mensagem por landerson

Sex Abr 24, 2015 10:32
Cálculo: Limites, Derivadas e Integrais
-
- Questão envolvendo derivadas:
por arthurvct » Qui Mai 16, 2013 17:15
- 2 Respostas
- 1591 Exibições
- Última mensagem por arthurvct

Qui Mai 16, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Questão envolvendo prova e angulo
por RuuKaasu » Sáb Dez 26, 2015 23:57
- 0 Respostas
- 1728 Exibições
- Última mensagem por RuuKaasu

Sáb Dez 26, 2015 23:57
Cálculo: Limites, Derivadas e Integrais
-
- Questão envolvendo Derivadas e área! Prova no sábado!!
por arthurvct » Qui Jun 13, 2013 15:21
- 1 Respostas
- 1630 Exibições
- Última mensagem por e8group

Sex Jun 14, 2013 00:49
Cálculo: Limites, Derivadas e Integrais
-
- Problema envolvendo função
por marianacarvalhops » Sáb Mai 02, 2009 17:46
- 1 Respostas
- 4425 Exibições
- Última mensagem por Marcampucio

Sáb Mai 02, 2009 18:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
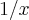 e g(x)=
e g(x)= , no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?
, no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?
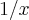 e g(x)=
e g(x)= , no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?
, no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?e g(x)=
, no ponto de interseção dos gráficos destas curvas. Qual o ângulo entre estas retas?

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)