 por Jhonata » Qui Mai 02, 2013 16:09
por Jhonata » Qui Mai 02, 2013 16:09
Estou com o seguinte problema em mãos, aparentemente bem simples:
Assinale a solução geral do sistema linear representado pela matriz aumentada
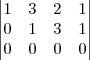
a)
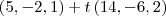
b)
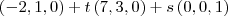
c)
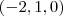
d)
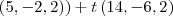
A alternativa b e c são falsas; na matriz, nitidamente tenho apenas uma linha nula, o que vai nos dar uma variável independente e teremos como conjunto solução uma reta(que no ponto de vista geral, o sistema terá infinitas soluções). Cara, eu terminei de escalonar(pra matriz totalmente escalonada) a matriz e parametrizei as equações lineares:
~
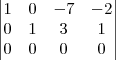
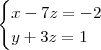
Fazendo z = t (o parâmetro, ou seja, a variável livre.):
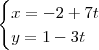
Dai o conjunto solução seria a reta:

{
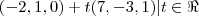
}
Que não bate com nenhuma das alternativas do gabarito que é a alternativa
a.
Mas vemos algo em comum na minha resposta com relação ao gabarito.
1)o vetor do espaço gerado é metade do que aparece no gabarito;
2) o vetor (-2,1,0) aparece no gabarito.
No que posso ter errado? Me corrijam, por favor. Qualquer ajuda é bem vinda. Grato desde já.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por e8group » Qui Mai 02, 2013 16:56
por e8group » Qui Mai 02, 2013 16:56
Sua solução está correta . No entanto ,qualquer vetor não nulo paralelo ao vetor diretor também é vetor diretor da reta . Assim , o vetor
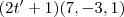
é diretor da reta .Onde :
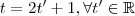
.
Além disso , note que :
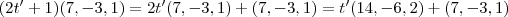
.
Daí ,
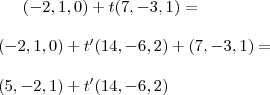
. Isto mostra que seus cálculos estão corretos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Qui Mai 02, 2013 17:26
por Jhonata » Qui Mai 02, 2013 17:26
Excelente explicação, mas ainda permaneceram duas dúvidas:
Como encontrar o vetor diretor?
E como eu saberia/notaria que deveria encontrá-lo pra utilizar no problema em questão?
Ah, muito obrigado mesmo pela ajuda!
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por e8group » Qui Mai 02, 2013 18:01
por e8group » Qui Mai 02, 2013 18:01
Jhonata escreveu:Como encontrar o vetor diretor?
Se uma reta passa pelos pontos

e

qualquer vetor que é múltiplo escalar de

será paralelo a

, ou seja , qualquer vetor que é múltiplo escalar de

será vetor diretor desta reta .(*) A escolha deste vetor irá influenciar no parâmetro ,por exemplo ,enquanto tomando-se

obtemos que o ponto
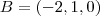
pertence a reta ,por outro lado ,tomando-se
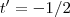
obterá
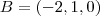
.
Jhonata escreveu:E como eu saberia/notaria que deveria encontrá-lo pra utilizar no problema em questão?
Está pergunta não sei responder ,geralmente quando a questão é múltipla escolha podemos verificar se a solução é equivalente a uma das alternativas . Neste caso , é fácil ver que o vetor
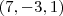
é múltiplo escalar de
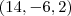
,pelo argumento (*) ,podemos ver que a mudança de variável
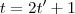
nos levará a resposta que está no formato do item (a) .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações diferenciais: solução geral
por emsbp » Sáb Abr 07, 2012 18:01
- 1 Respostas
- 896 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 07, 2012 19:03
Cálculo: Limites, Derivadas e Integrais
-
- [Equação Diferencial] Grau de homogeneidade e solução geral
por kayone » Dom Set 22, 2013 17:37
- 1 Respostas
- 1665 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 23:49
Equações
-
- Encontrar a Equação Geral do Plano
por Vitor2+ » Seg Nov 14, 2011 02:21
- 7 Respostas
- 10663 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:04
Geometria Analítica
-
- Inequação - encontrar conjunto solução
 por rafaleans » Sex Mar 14, 2014 09:45
por rafaleans » Sex Mar 14, 2014 09:45
- 1 Respostas
- 1624 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 19, 2014 22:56
Inequações
-
- Equação Logarítmica - Não consigo encontrar a Solução !
por Kirie » Seg Out 04, 2010 22:27
- 3 Respostas
- 2100 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 23:34
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
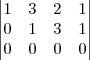
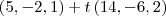
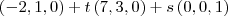
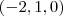
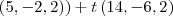
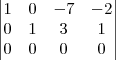
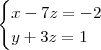
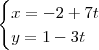
 {
{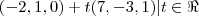 }
}

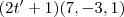 é diretor da reta .Onde :
é diretor da reta .Onde : 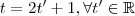 .
.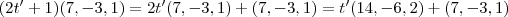 .
. 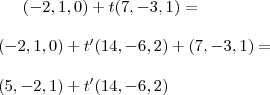 . Isto mostra que seus cálculos estão corretos .
. Isto mostra que seus cálculos estão corretos .
 e
e  qualquer vetor que é múltiplo escalar de
qualquer vetor que é múltiplo escalar de  será paralelo a
será paralelo a  obtemos que o ponto
obtemos que o ponto 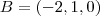 pertence a reta ,por outro lado ,tomando-se
pertence a reta ,por outro lado ,tomando-se 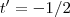 obterá
obterá 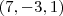 é múltiplo escalar de
é múltiplo escalar de 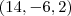 ,pelo argumento (*) ,podemos ver que a mudança de variável
,pelo argumento (*) ,podemos ver que a mudança de variável 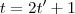 nos levará a resposta que está no formato do item (a) .
nos levará a resposta que está no formato do item (a) .




