O jornal Folha de S.Paulo publicou em 21.06.2007 o seguinte
artigo:
Tarifas bancarias
Mádia das taxas cobradas pelos dez maioes bancos do país pelos serviços.Manuteção de conta corrente especial ativa.Taxa mensal,em R$:
2005=6,31
2006=7,14
2007=8;13
De acordo com a informação publicada nesse artigo,as médias das taxas mensais para a manutenção de uma conta corrente especial ativa aumentam,de 2005 para 2007,aproximadamente
a)13,8%
b)17,3%
c)20,5%
d)26,9%
e)28,8%
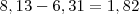
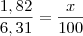
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)