 por Jhennyfer » Qui Abr 25, 2013 13:51
por Jhennyfer » Qui Abr 25, 2013 13:51
oi, preciso de uma mãozinha...
A expressão mais simples para
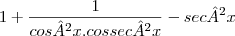
é:
iniciei resolvendo assim, inverso de cosseno é secante, e inverso de cossecante é seno, portanto:
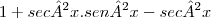
Agora não consigo resolver a parte da multiplicação sec²x.sen²x, se é que está certo!
esse  não sei pq está aparecendo na formula, se isto estiver errado desconsidere. obg

-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Abr 25, 2013 15:32
por e8group » Qui Abr 25, 2013 15:32
Você pensou corretamente sobre a questão .Entretanto ,note que
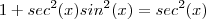
(Por quê ?) .Assim ,
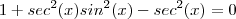
.
Observações :
i)
Lembrando que
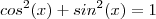
( identidade trigonométrica fundamental)
Pergunta :O que acontece se dividirmos cada lado da igualdade por
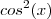
ou se multiplicarmos ambos lados da igualdade por
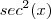
?
ii)
Para digitar expressões do tipo a² + b² em
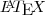
o correto é digitar a^2 +b^2 entre .
Compare os resultados :
a² + b² produz

em
a^2 +b^2 produz

em
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Qui Abr 25, 2013 16:07
por Jhennyfer » Qui Abr 25, 2013 16:07
eu entendi, mas não to conseguindo terminar a questão =/
a resposta é 0
o que eu faço depois de
1+sec²x.sen²x-sec²x=0
?????????
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Abr 25, 2013 16:30
por e8group » Qui Abr 25, 2013 16:30
O que deverá fazer é responde a pergunta que fiz na observação ,isto é ,
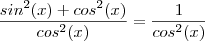
que é equivalente a
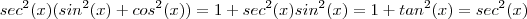
. Daí ,
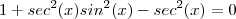
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações
por Rose » Qui Mai 15, 2008 14:41
- 1 Respostas
- 1957 Exibições
- Última mensagem por admin

Qui Mai 15, 2008 16:38
Funções
-
- Relações
por chronoss » Seg Mai 20, 2013 14:19
- 0 Respostas
- 1042 Exibições
- Última mensagem por chronoss

Seg Mai 20, 2013 14:19
Álgebra Elementar
-
- Relações
por livia02 » Qua Set 04, 2013 17:15
- 0 Respostas
- 1116 Exibições
- Última mensagem por livia02

Qua Set 04, 2013 17:15
Álgebra Elementar
-
- [Relações]
por Giudav » Ter Fev 11, 2014 18:38
- 1 Respostas
- 2553 Exibições
- Última mensagem por DanielFerreira

Qua Fev 12, 2014 17:47
Sequências
-
- Relações no círculo
por RBenicio » Qua Set 16, 2009 15:34
- 3 Respostas
- 2821 Exibições
- Última mensagem por Molina

Qui Set 17, 2009 14:45
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
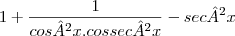 é:
é: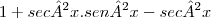


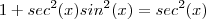 (Por quê ?) .Assim ,
(Por quê ?) .Assim ,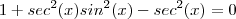 .
. 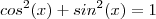 ( identidade trigonométrica fundamental)
( identidade trigonométrica fundamental) 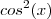 ou se multiplicarmos ambos lados da igualdade por
ou se multiplicarmos ambos lados da igualdade por 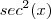 ?
? 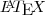 o correto é digitar a^2 +b^2 entre .
o correto é digitar a^2 +b^2 entre . em
em  em
em 
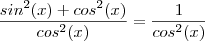 que é equivalente a
que é equivalente a 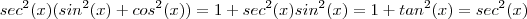 . Daí ,
. Daí ,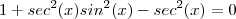 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
