Sei que para provar que um certo limite de duas variáveis não existe, basta tomar o limite dessa função através de dois caminhos distintos, ou seja, de duas curvas, de forma que esses limites sejam diferentes. Prova-se assim, que não existe limite naquele ponto (xo,yo) para o qual tende o limite, isso é, xo,yo é um ponto de descontinuidade da superfície..
Eu resolvi vários exercícios sobre aqui, e todos eu conseguia resolver de forma trivial, tomando curvas como
g:(0,t)
g:(t,t)
g:(0,t²)
g:(t, at)
enfim, coisas 'fáceis' de ir testando..
Porém, como fazer para "descobrir uma curva" para usar nesse 'teste', quando ela precisa ser um pouco mais elaborada?
exemplo:
o professor resolveu este assim:
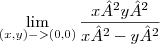
tome a curva c1(t) = (t,0)
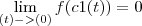(esse limite converge para zero)tome agora a curva c2(t) =
![(\sqrt[2]{t²+t^4} , t)](/latexrender/pictures/4f9406e6f9d831a1288c02e815f4117a.png "(\sqrt[2]{t²+t^4} , t)")
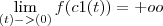(esse limite diverge)como conseguimos valores diferentes para a função quando x,y se aprovima de (0,0) por diferentes caminhos, o limite não existe.
Como ele chegou nessa curva c2? Qual motivação ele teve de testar justamente ela? Existe algum método prático para isso? Algum macete?
Valeu pessoal.
