 por arthurvct » Ter Abr 23, 2013 14:50
por arthurvct » Ter Abr 23, 2013 14:50
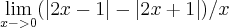
, alguém por favor faz passo a passo? Vai me ajudar muito!
-
arthurvct
-
 por arthurvct » Ter Abr 23, 2013 15:26
por arthurvct » Ter Abr 23, 2013 15:26
up!!!!
-
arthurvct
-
 por e8group » Ter Abr 23, 2013 16:59
por e8group » Ter Abr 23, 2013 16:59
Por definição de módulo ,
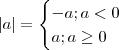
. Assim ,
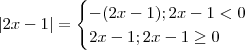
e
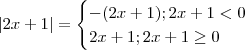
Como
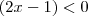
e
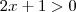
quando

se aproxima de zero .Então ,
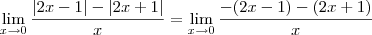
.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por arthurvct » Ter Abr 23, 2013 17:18
por arthurvct » Ter Abr 23, 2013 17:18
ah entendi! dá -4??
-
arthurvct
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Modular. Ajudem por favor
por zenildo » Seg Mai 02, 2016 22:50
- 1 Respostas
- 1541 Exibições
- Última mensagem por nakagumahissao

Qua Mai 04, 2016 08:30
Funções
-
- Limite- Função modular
por killerkill » Sáb Ago 20, 2011 13:18
- 9 Respostas
- 12385 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 17:18
Cálculo: Limites, Derivadas e Integrais
-
- LIMITE- Ajudem
 por Rafael Zanelato » Seg Mar 31, 2014 14:17
por Rafael Zanelato » Seg Mar 31, 2014 14:17
- 3 Respostas
- 1787 Exibições
- Última mensagem por Man Utd

Ter Abr 01, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Sex Out 23, 2009 20:36
- 1 Respostas
- 2431 Exibições
- Última mensagem por Tom

Sáb Jul 03, 2010 21:30
Sequências
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Qua Out 28, 2009 23:47
- 0 Respostas
- 1393 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
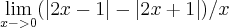 , alguém por favor faz passo a passo? Vai me ajudar muito!
, alguém por favor faz passo a passo? Vai me ajudar muito!

 . Assim ,
. Assim , 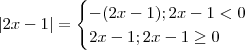
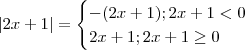
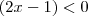 e
e 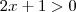 quando
quando  se aproxima de zero .Então ,
se aproxima de zero .Então , 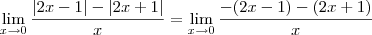 .
. 