![\int_{0}^{2}\sqrt[2]{1-4{x}^{2}}](/latexrender/pictures/949cafffdeabd07897cf75097c570402.png "\int_{0}^{2}\sqrt[2]{1-4{x}^{2}}")
tenho que resolver essa integral através de substituições trigonométricas,onde eu sei que
![\sqrt[2]{a-{x}^{2}} => x= asen\theta,dx=acos\theta](/latexrender/pictures/7bc8468ab326162f9f4ba69db75a6e33.png "\sqrt[2]{a-{x}^{2}} => x= asen\theta,dx=acos\theta")
porém neste caso meu "X" esta sendo multiplicado por 4 como eu resolvo isto? Antes de vim postar minha duvida aqui eu tentei fazer o seguinte
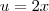
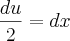
depois disso me deu um nó "mental"
e não conseguir sair dai.Se alguém puder me ajudar a sair dali ficaria muito grato. obg
.
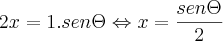![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)